Решение обратной геодезической задачи
Задача ставится так, что требуется вычислить расстояние и дирекционный угол для двух точек, заданных своими координатами (рис. 6).
ратной геодезической задачи.
Из рисунка видно, что для тангенса дирекционного угла можно записать соотно-
шение:
tg a = y 2 - y 1.
x 2 - x 1
Значит для угла a = arctg (y 2 - y 1 ). При проведении конкретных
x 2 - x 1
S 1 - 2 = (y 2 - y 1) + (x 2 - x 1). Тестовый пример: для исходных данных x1 =6; y1 =5; x2 =1; y2 =3 расчет дает: a 1-2=201о48.1', S1-2=5.39. Начало
Нет
y 2 - y 1 < 0
Да нет
a = 2 p + arctan(y 2 - y 1) a = arctan(y 2 - y 1) 1 - 2 x 2 - x 1 1 - 2 x 2 - x 1
a = p + arctan(y 2 - y 1) 1 - 2 x 2 - x 1
Конец
Решение обратной угловой засечки по формулам Пранис- Праневича Задача ставится так, что требуется вычислить координаты
Рис. 8. Схема для вычисления по форму- лам Пранис-Праневича.
Расчет неизвестных коорди- нат точки Р может быть произведен по формулам Пранис-Праневича:
(x 2 - x 1) ctg a - (x 3 - x 2) ctg b - y 1 + y 3 N = (y 2 - y 1)(ctg a - tgQ) - (x 2 - x 1)(1 + ctg a tgQ);
D x = N
; D y = D x tgQ; x p = x 2 + D x; y p = y 2 + D y. Тестовый пример: для исходных данных x1 =3, y1 =1; x2 =1, y2 =4; x3 =2, y3 =7; a=20о15.3', b=19о01.0' расчет дает xp =10.37; yp =2.28.
|

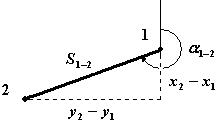 Рис. 6. Схема для решения об-
Рис. 6. Схема для решения об- 1 - 2
1 - 2 1-2
1-2
 Рис. 7. Схема для выбора формулы для вычисления угла.
Рис. 7. Схема для выбора формулы для вычисления угла. точки Р по координатам трех заданных точек и двум углам (рис. 8).
точки Р по координатам трех заданных точек и двум углам (рис. 8). (y - y) ctg a - (y - y) ctg b + x - x tgQ = 2 1 3 2 1 3;
(y - y) ctg a - (y - y) ctg b + x - x tgQ = 2 1 3 2 1 3; 1 + tg 2 Q
1 + tg 2 Q


