Основы химической термодинамики. − Математическое выражение для первого начала термодинамики
− Математическое выражение для первого начала термодинамики Q = DU+A,(2.1.1) где DU – изменение внутренней энергии системы; Q – теплота, поглощенная или выделенная системой; А – полная работа, равная сумме работы расширяющегося газа (pDV) и полезной работы А ', включающей в себя все другие виды работы, кроме работы расширяющегося газа. − Тепловой эффект реакции при постоянном давлении в стандартных условиях равен изменению стандартной энтальпии системы в ходе реакции. На основании следствия из закона Гесса энтальпия реакции может быть рассчитана, исходя из табличных величин стандартных энтальпий образования исходных веществ и продуктов реакции, по уравнению
где
Для органических веществ часто в расчетах используют справочные значения теплот сгорания, тогда
− Тепловой эффект реакции при постоянном объеме QV=DU (2.1.4) Qp= QV+DvRT, (2.1.5) где Dv – изменение числа моль газообразных веществ в ходе реакции
Определение работы в различных процессах − Изохорный процесс: А=0; − Изобарный процесс: A=pΔV; (2.1.6) − Изотермический процесс (для произвольного числа моль ν идеального газа):
− Адиабатический процесс:
где СV – молярная теплоемкость при постоянном объеме. Если СV не зависит от температуры, то
− Энтропия реакции
− Энергия Гиббса реакции
− Изменение энергии Гиббса (изобарно-изотермического потенциала) в ходе процесса DG=DH-TDS (2.1.11) − Изменение энергии Гельмгольца (изохорно-изотермического потенциала) в ходе процесса DF=DU-TDS (2.1.12) − Основное уравнение второго начала термодинамики
− Условие самопроизвольного протекания процесса в закрытых системах при изобарно-изотермических условиях DG˂;0 (2.1.14) − Условие самопроизвольного протекания процесса в закрытых системах при изохорно-изотермических условиях DF˂;0 (2.1.15) − Уравнение Кирхгофа в дифференциальной форме для изобарных условий:
где Ср – молярная теплоемкость при постоянном давлении.
− Уравнение Кирхгофа в интегральной форме для изобарных условий:
Если в заданном температурном интервале происходят фазовые переходы и образование новых полиморфных форм веществ, то
− Зависимость теплоемкости от температуры Зависимость теплоемкости от температуры обычно выражают в виде интерполяционных уравнений, коэффициенты в которых получают эмпирически или на основании молекулярно-статистических расчетов. Эти коэффициенты приводятся в справочниках. Для органических веществ: Для неорганических веществ:
− Температурная зависимость энтропии
Для изменения энтропии в ходе некоторого процесса, если известно изменение энтропии при стандартных условиях, формулу (2.1.19) можно представить в следующем виде:
|

 , (2.1.2)
, (2.1.2) - коэффициенты в химическом уравнении при соответствующих продуктах реакции;
- коэффициенты в химическом уравнении при соответствующих продуктах реакции; - коэффициенты в химическом уравнении при соответствующих исходных веществах;
- коэффициенты в химическом уравнении при соответствующих исходных веществах; - стандартные энтальпии образования соответствующих веществ.
- стандартные энтальпии образования соответствующих веществ.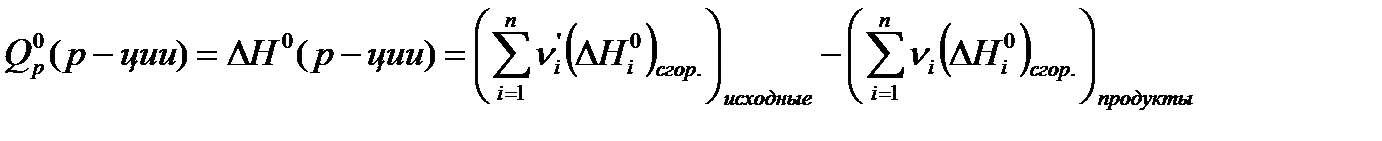 (2.1.3)
(2.1.3)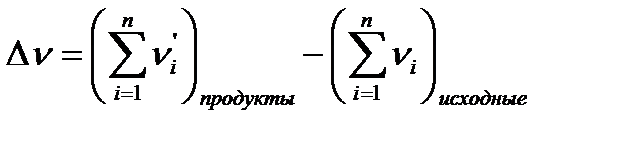
 ; (2.1.7)
; (2.1.7) , (2.1.8)
, (2.1.8) .
. (2.1.9)
(2.1.9) (2.1.10)
(2.1.10)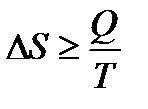 (2.1.13)
(2.1.13) , (2.1.16)
, (2.1.16) (2.1.17)
(2.1.17)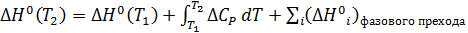 (2.1.18)
(2.1.18) .
. .
. (2.1.19)
(2.1.19) (2.1.20)
(2.1.20)


