Поверхностные явления и адсорбция. Для характеристики раздробленности дисперсных систем используют следующие величины:
Для характеристики раздробленности дисперсных систем используют следующие величины: а – определяющий (минимальный) линейный размер элементов дисперсной фазы (диаметр нити, диаметр сферы, толщина пленки, ребро куба); дисперсность удельная поверхность – отношение площади поверхности дисперсной фазы к ее объему, либо ее массе:
Аналогичные формулы используются и при нахождении удельной поверхности одной усредненной частицы:
Чем больше степень измельчения, тем меньше размер частиц, больше дисперсность и удельная поверхность. Атомы или молекулы, находящиеся на поверхности раздела фаз, энергетически отличаются от тех, которые находятся в объеме фазы, они обладают некоторой избыточной энергией. Если рассматриваются изобарно-изотермические условия, то поверхность раздела фаз характеризуется избыточной свободной энергией Гиббса или просто поверхностной энергией. Поверхность раздела фаз также характеризуется удельной поверхностной энергией
и поверхностным натяжением s. Существует энергетическая и силовая трактовка этой величины. С энергетических позиций это работа, затрачиваемая в изобарно-изотермических условиях на обратимое образование 1м2 поверхности раздела фаз, то есть поверхностное натяжение равно изменению энергии Гиббса в этом процессе:
Процессы, протекающие на границе раздела фаз, называются поверхностными явлениями. К ним можно отнести смачивание, адгезию, капиллярные явления, адсорбцию и другие. Смачивание – это поверхностное явление, заключающееся во взаимодействии жидкости с твердым телом или с другой жидкостью при наличии одновременного контакта трех несмешивающихся фаз, одной из которых является воздух. Рассмотрим смачивание жидкостью поверхности твердого тела. В этом случае можно наблюдать три процесса: - нанесенная капля растекается (процесс растекания); - нанесенная жидкость остается в виде прилипшей капли (смачивание); - нанесенная жидкость стягивается, образуя шар (несмачивание). Количественной характеристикой степени смачивания поверхности является краевой угол смачивания. Краевой угол θ; определяется как угол между касательной, проведенной к поверхности смачивающей жидкости, и смачиваемой поверхностью твердого тела, причем угол всегда отсчитывается в сторону жидкой фазы. Касательную проводят через точку соприкосновения трех фаз. На рисунке 2.6.1 показано построение краевого угла смачивания. Равновесное значение краевого угла можно выразить через поверхностное натяжение по формуле Юнга:
Жидкость не смачивает поверхность, если θ>90о. В этом случае поверхность является лиофобной (гидрофобной в случае воды). Если жидкость смачивает поверхность, то θ<90о. Такая поверхность является лиофильной (гидрофильной в случае воды).
а
Рисунок 2.6.1 – Краевой угол при: а – смачивании; б – несмачивании.
Адгезия (прилипание) – это взаимодействие между приведенными в контакт поверхностями конденсированных фаз разной природы за счет различных физических или химических межмолекулярных сил. Работа адгезии может быть выражена через поверхностное натяжение взаимодействующих фаз и межфазное натяжение (уравнение Дюпре):
Подставляя в уравнение Дюпре формулу Юнга, получаем уравнение
Если происходит искривление поверхности, то свойства поверхостного слоя изменяются. Это приводит к возникновению избыточного поверхностного давления (капиллярного давления). Сила капиллярного давления направлена к центру кривизны поверхности. Поэтому, если жидкость смачивает стенки капилляра (вогнутый мениск), она будет подниматься по капилляру вверх. Если капилляр поместить в несмачивающую его стенки жидкость (выпуклый мениск), то произойдет опускание уровня жидкости в капилляре ниже уровня жидкости в сосуде. Если упрощенно считать, что мениск представляет собой полусферу (так бывает при полном смачивании или полном несмачивании), то рассчитать высоту поднятия (или опускания) h жидкости в капилляре можно по упрощенной формуле:
где s – поверхностное натяжение; r – радиус капилляра; g – ускорение свободного падения; ρ – плотность жидкости. Существуют такие вещества, при добавлении которых в раствор, существенно снижается поверхностное натяжение растворителя. Такие добавки называются поверхностно-активными веществами (ПАВ). По отношению к воде – это органические кислоты, спирты, амины, белки, мыла и другие дифильные вещества, молекулы которых состоят из полярной гидрофильной части и гидрофобного углеводородного радикала. Если в качестве ПАВ используются водные растворы высших карбоновых кислот, то зависимость поверхностного натяжения от молярной концентрации раствора выражается эмпирическим уравнением Шишковского (хотя это уравнение можно вывести и теоретически на основании изотерм адсорбции Гиббса и Ленгмюра):
где s0 – поверхностное натяжение чистого растворителя; а – эмпирическая константа, одинаковая для всех членов гомологического ряда (приблизительно 0,2 при 200С); b – константа, зависящая от поверхностной активности вещества, она из меняется в гомологическом ряду в соответствии с правилом Дюкло-Траубе: увеличивается в 3 – 3,5 раза для каждого последующего члена ряда. Поверхностная активность вещества определяется производной поверхностного натяжения по концентрации, взятой с отрицательным знаком:
Поверхностная активность вещества может быть определена графическим дифференцированием, если имеется экспериментальная зависимость поверхностного натяжения от концентрации. Для этого строится график в координатах s - С и для линейного участка определяется тангенс угла наклона к оси абсцисс. Из геометрического смысла производной он равен Адсорбция – это самопроизвольное изменение концентрации в поверхностном слое по сравнению с его концентрацией в объеме фазы. Чаще всего приходится иметь дело с положительной адсорбцией, приводящей к увеличению концентрации вещества в поверхностном слое (например, адсорбция растворенных веществ и газов на твердых телах, адсорбция ПАВ из раствора). Но есть также случаи отрицательной адсорбции – уменьшение концентрации поверхностно-инактивных веществ (ПИВ) в поверхностном слое. Количественно адсорбция Г может быть выражена величиной количества вещества адсорбата (в моль или кмоль), приходящейся на 1м2 поверхности адсорбента. Если величину площади поверхности определить не удается, то количество адсорбата относят к массе адсорбента. Зависимость адсорбции от концентрации или парциального давления адсорбата при постоянной температуре выражается уравнениями, названными изотермами адсорбции. Уравнение изотермы адсорбции Гиббса устанавливает соотношение между величиной адсорбции Г, выраженной в кмоль/м2, концентрацией раствора С (кмоль / м3) и поверхностной активностью
где R – универсальная газовая постоянная; Т – абсолютная температура, К. Уравнение изотермы монослойной адсорбции Ленгмюра:
где α – константа адсорбционного равновесия. Если адсорбция происходит из газовой фазы, то концентрация в уравнении Ленгмюра заменяется на равновесное парциальное давление газа. Продифференцировав уравнение Шишковского, получам:
Если это выражение подставить в уравнение Гиббса и сравнить полученный результат с уравнением Ленгмюра, то окажется, что константа α в уравнении Ленгмюра и константа b в уравнении Шишковского совпадают, а величина предельной адсорбции Общий вид изотермы адсорбции Ленгмюра представлен на рисунке 2.6.2
Г Г
Г∞
С С
а) б)
Рисунок 2.6.2 – Общий вид изотерм адсорбции: а) изотерма Ленгмюра; б) изотерма Фрейндлиха
Уравнение изотермы Фрейндлиха (2.6.14) было предложено задолго до работ Ленгмюра. Это уравнение носит эмпирический характер.
где k – эмпирическая константа, зависящая от природы адсорбента, изменяется в широких пределах; n – эмпирическая константа, зависящая от температуры и природы адсорбата, принимает значения от 1 до 10 Общий вид изотермы Фрейндлиха представлен на рисунке 2.6.2. Изотерма Фрейндлиха отличается от изотермы Ленгмюра отсутствием области насыщения. Уравнение Фрейндлиха хорошо согласуется с экспериментальными данными только в области средних концентраций адсорбата. Оно становится неприменимым в тех случаях, когда уже при небольших концентрациях наблюдается предел адсорбции. Константы в уравнениях Лэнгмюра и Фрейндлиха можно определить графическим методом. Для нахождения констант Г∞ и α; уравнение Ленгмюра приводят к линейному виду (у=кх+в). Для этого левую и правую части уравнения (2.6.12) возводят в степень -1 и приводят к виду (2.6.15).
В координатах В уравнении (2.6.15) угловому коэффициенту соответствует
у β в х
Рисунок 2.6.3 – Зависимость
В соответствии с рисунком 2.6.3,
в Для того чтобы определить константы k и n в уравнении Фрейндлиха, формулу (2.6.14) логарифмируют и приводят к виду (2.6.16)
Построив график зависимости
у β в х
Рисунок 2.6.4 – Зависимость
В соответствии с рисунком 2.6.4,
в
|

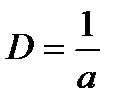 ;
; ;
;  (2.6.1)
(2.6.1) ;
;  (2.6.2)
(2.6.2) ;
;  (2.6.3)
(2.6.3) (2.6.4)
(2.6.4) ;
;  (2.6.5)
(2.6.5) (2.6.6)
(2.6.6)
 (2.6.7)
(2.6.7) (2.6.8)
(2.6.8) , (2.6.9)
, (2.6.9) , (2.6.10)
, (2.6.10)
 .
. , (2.6.11)
, (2.6.11) , (2.6.12)
, (2.6.12)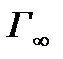 – максимальная (предельная) адсорбция, кмоль / м3;
– максимальная (предельная) адсорбция, кмоль / м3; . (2.6.13)
. (2.6.13) .
. , (2.6.14)
, (2.6.14) (2.6.15)
(2.6.15) график этого уравнения представляет собой прямую линию. Обратимся к рисунку 2.6.3. На основании свойств линейной функции у=кх+в тангенс угла наклона β прямой к оси абсцисс равен угловому коэффициенту к, а отрезок, отсекаемый прямой на оси ординат, равен в.
график этого уравнения представляет собой прямую линию. Обратимся к рисунку 2.6.3. На основании свойств линейной функции у=кх+в тангенс угла наклона β прямой к оси абсцисс равен угловому коэффициенту к, а отрезок, отсекаемый прямой на оси ординат, равен в. , а параметру в соответствует
, а параметру в соответствует  .
.

 ;
;
 (2.6.16)
(2.6.16) , получим прямую линию, как показано на рисунке (2.6.4).
, получим прямую линию, как показано на рисунке (2.6.4).


 ;
;



