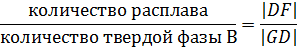Фазовые равновесия

 

Компонентом называется химически однородная часть системы, которая может быть выделена из системы в виде индивидуального вещества. Например, водный раствор Na₂CO₃ и NaCl состоит из трех компонентов: воды, карбоната натрия и хлорида натрия.

Число независимых компонентов (К) – это число, равное общему числу компонентов системы за вычетом числа химических реакций, связывающих эти компоненты. В случае исключительно фазового равновесия число независимых компонентов равно общему числу компонентов.

Число степеней свободы (С) – это число внешних факторов, которые можно изменять в известных пределах без изменения числа и вида фаз.

Число внешних условий (n) – число тех факторов, которые влияют на состояние равновесия. Обычно это температура и давление (n =2), если же давление не влияет на смещение равновесия, то n =1.

Правило фаз Гиббса: число степеней свободы (С), число фаз (Ф), число независимых компонентов (К) и число внешних условий (n), влияющих на равновесие, связаны соотношением

С+Ф=К+n. (2.3.1)

Определение относительного количества расплава и твердой фазы по диаграмме плавкости двухкомпонентной системы проводится с помощью правила рычага: отношение количеств равновесных фаз обратно отношению отрезков, отсекаемых ординатой температуры на участке общего состава смеси, лежащем внутри области двухфазного равновесия. Например, в соответствии с рисунком 2.3.1, можно записать:

 

Тпл В

Тпл А

D

G

P=const

Рисунок 2.3.1 – Диаграмма плавкости двухкомпонентной системы

 

Для построения диаграммы состояния трехкомпонентной системы требуется четыре координаты: давление, температура, доли двух компонентов из трех, отражающие состав системы.

Для представления состояния трехкомпонентной системы на плоскости необходимо принять условие постоянства температуры и давления. Состав же тройной системы удобно выражать при помощи треугольной диаграммы Гиббса-Розебома, показанной на рисунке 2.3.2.

Вершины равностороннего треугольника соответствуют чистым веществам А, В и С. Точки на сторонах треугольника отвечают составам двухкомпонентных систем А-В, А-С, В-С. Каждая точка внутри треугольника отражает состав тройной смеси.

Существует два метода определения состава по треугольной диаграмме. По методу Гиббса за 100% принимается высота правильного треугольника. При этом сумма длин перпендикуляров, опущенных из любой точки внутри треугольника на его стороны, есть величина постоянная, равная высоте этого треугольника.

Процентное содержание каждого компонента определяется расстоянием от точки Р, отражающей состав системы, до стороны треугольника, противолежащей вершине, соответствующей чистому компоненту.

 

Рисунок 2.3.2 – Выражение состава трехкомпонентной системы: а) по методу Гиббса; б) по методу Розебома

 

На рисунке 2.3.2а отрезок Р а соответствует процентному содержанию компонента А, отрезок Р b – содержанию компонента В, отрезок Р с – содержанию компонента С.

По методу Розебома (рисунок 2.3.2б) за 100% принимается длина стороны правильного треугольника. Сумма длин трех отрезков, проведенных параллельно сторонам треугольника из точки Р (Р а+ Р b+ Р с) равна стороне треугольника. Содержание компонента А соответствует длине отрезков Р а=bc=b'B=ac, соержание компонента В соответствует длине отрезков Pb=a'b=Ac=c'C, для компонента С содержание соответствует длине отрезков pc=Aa'=cb'=BA.

Оба метода приводят к одинаковым результатам, так как стороны и высоты равностороннего треугольника пропорциональны друг другу.