Оптические свойства дисперсных систем
Дисперсные системы обладают свойством рассеивать свет. Для систем с непроводящими частицами сферической формы, радиус которых меньше длины волны падающего света при их небольшой концентрации для единицы объема выполняется уравнение Рэлея:
где IР и I0 – интенсивности рассеянного и падающего света соответственно; N – численная (или частичная) концентрация (число частиц в единице объема); V – объем частицы; λ; – длина волны падающего света; n1 и n0 – показатели преломления дисперсной фазы и дисперсионной среды соответственно. Мутность системы – это характеристика, определяемая соотношением:
Обратная величина называется светорассеянием. Массовая концентрация может быть рассчитана как произведение частичной концентрации, объема частицы и ее плотности:
С учетом выражения (2.7.3) для данных условий измерения светорассеяния уравнение (2.7.1) принимает вид
где k – константа для данных условий измерения. Формулы (2.7.4) лежат в основе расчетов нефелометрического анализа. Если объем частиц для двух систем, анализируемых в одинаковых условиях, одинаков, то
Если же сравниваются две системы с одинаковой концентраций, то можно определить размеры частиц:
Нефелометрия позволяет сравнивать мутности двух систем, концентрация или дисперсность одной из которых известна. Освещая кюветы с золями равномерно падающим светом и меняя высоту освещенной части золей h1 и h2, добиваются равенства интенсивности света, рассеянного обоими золями, тогда справедливы равенства:
При прохождении света через коллоидно-дисперсную систему наблюдается также светопоглощение. При малых концентрациях и малой толщине слоя выполняется закон Бугера-Ламберта-Бера:
где Iпр и I0 – интенсивность прошедшего через раствор света и интенсивность падающего света соответственно; ε – молярный коэффициент светопоглощения; С – массовая концентрация раствора, г/л; l – толщина слоя раствора. Логарифмирование выражения (2.7.8) дает формулу для оптической плотности (экстинкции) D:
Справедливость закона Бугера-Ламберта-Бера подтверждается постоянством величины При решении графических задач этого раздела нужно учитывать то, что выражение (2.7.9) в координатах Для бесцветных разбавленных золей, в которых отсутствует поглощение света и вторичное светорассеяние, рассеянный системой свет можно рассматривать как фиктивно поглощенный. Тогда можно воспользоваться законом Бугера-Ламберта-Бера, придав его выражению следующий вид:
где t - мутность; l – толщина слоя системы; D – оптическая плотность. Турбидиметрия базируется на измерении оптической плотности. При сравнении оптических плотностей стандартного и исследуемого золей в одинаковых условиях справедливы выражения: при одинаковом размере частиц и одинаковой длине волны падающего света
где N – частичная концентрация; при одинаковой концентрации
Таким образом, этот метод позволяет определить концентрации и размеры частиц.
|

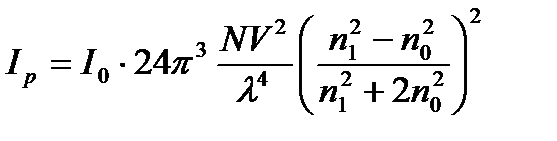 , (2.7.1)
, (2.7.1) . (2.7.2)
. (2.7.2) (2.7.3)
(2.7.3) , (2.7.4)
, (2.7.4) (2.7.5)
(2.7.5) (2.7.6)
(2.7.6) ;
;  ;
;  (2.7.7)
(2.7.7) , (2.7.8)
, (2.7.8) (2.7.9)
(2.7.9) (2.7.10)
(2.7.10) (2.7.11)
(2.7.11) для данной системы при различных значениях интенсивности прошедшего света.
для данной системы при различных значениях интенсивности прошедшего света. от С или
от С или  от l дает график прямой. Поэтому по величине отрезка, отсекаемого прямой на оси ординат, и по тангенсу угла наклона прямой к оси абсцисс можно определить соответствующие искомые величины: ln I0; ε; C.
от l дает график прямой. Поэтому по величине отрезка, отсекаемого прямой на оси ординат, и по тангенсу угла наклона прямой к оси абсцисс можно определить соответствующие искомые величины: ln I0; ε; C. или
или  , (2.7.12)
, (2.7.12) (2.7.13)
(2.7.13) (2.7.14)
(2.7.14)


