ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Изгиб с кручением
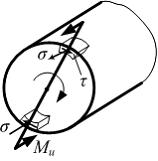
Стержень круглого сечения работает на кручение и изгиб. В опасных точках напряженное состояние …
|
|
| плоское
|
|
|
|
| линейное
|
|
|
|
| объемное
|
|
|
|
| чистый сдвиг
|
Решение:
При изгибе с кручением в опасных точках круглого поперечного сечения, расположенных у поверхности стержня, действуют максимальные нормальные и касательные напряжения. Грани элементарных объемов, совпадающих с поверхностью стержня, являются главными площадками с главными напряжениями равными нулю. Поэтому напряженное состояние в опасных точках плоское.
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Изгиб с растяжением?сжатием
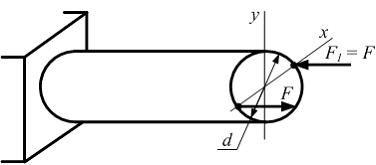
Стержень круглого сечения диаметром d нагружен двумя силами F и 
При смене направления силы 
на противоположное значение максимального нормального напряжения в поперечном сечении стержня …
|
|
|
| уменьшится в 4 раза
|
|
|
|
| уменьшится в 2 раза
|
|
|
|
| не изменится
|
|
|
|
| увеличится в 2 раза
|
Решение:
Стержень испытывает чистый изгиб моментом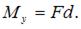 
Максимальное нормальное напряжение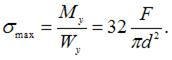 
При смене направления силы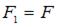 
на противоположное, стержень будет работать на растяжение силой 2 F.
Тогда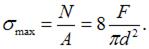 
Максимальное нормальное напряжение уменьшится в четыре раза.
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Пространственный и косой изгиб
Стержень прямоугольного сечения с размерами b и 2 b, длиной l нагружен моментом М. Плоскость действия момента расположена под углом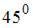 
к главным центральным осям сечения. Отношение значений нормальных напряжений в точках В и С равно …
ЗАДАНИЕ N 24 сообщить об ошибке
Тема: Виды нагружения стержня
При данном варианте нагружения стержень прямоугольного сечения с размерами b и 2 b испытывает …
|
|
|
| чистый косой изгиб и растяжение
|
|
|
|
| растяжение и кручение
|
|
|
|
| плоский поперечный изгиб
|
|
|
|
| растяжение и плоский поперечный изгиб
|
Решение:
Рассекаем стержень произвольным сечением на две части. Отбросим левую часть. Рассматривая равновесие правой части получим, что в поперечном сечении действуют три внутренних силовых фактора: продольная сила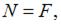 
два изгибающих момента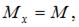 
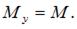
Таким образом, стержень испытывает растяжение и чистый косой изгиб.
ЗАДАНИЕ N 25 сообщить об ошибке
Тема: Продольная сила. Напряжения и деформации
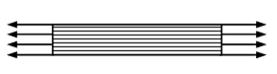
На рисунке показан растянутый стержень. Между продольными слоями материала …
|
|
|
| отсутствуют нормальные и касательные напряжения
|
|
|
|
| действуют нормальные напряжения
|
|
|
|
| действуют касательные напряжения
|
|
|
|
| действуют нормальные и касательные напряжения
|
ЗАДАНИЕ N 26 сообщить об ошибке
Тема: Испытание конструкционных материалов на растяжение и сжатие
Вид образца из пластичного материала после испытаний на сжатие показан на рисунке …
|
|
|
| d
|
|
|
|
| a
|
|
|
|
| b
|
|
|
|
| c
|
Решение:
Образец из пластичного материала при испытании на сжатие не разрушается, а только расплющивается, что и показано на рисунке «d».
ЗАДАНИЕ N 27 сообщить об ошибке
Тема: Механические свойства и механические характеристики материалов
При нагружении образца силами F стрелки тензометров А и В переместились на 10 делений, а стрелка тензометра С – на 3 деления. Базы тензометров – 20 мм. Цена деления шкалы тензометров – 0,001 мм. Коэффициент Пуассона материала образца по абсолютной величине равен …
|
|
|
| 0,3
|
|
|
|
| 0,25
|
|
|
|
| 0,4
|
|
|
|
| 0,35
|
Решение:
Продольная линейная деформация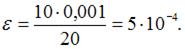 
Поперечная линейная деформация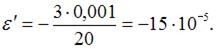 
Коэффициент Пуассона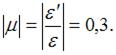 
ЗАДАНИЕ N 28 сообщить об ошибке
Тема: Расчеты стержней на прочность и жесткость
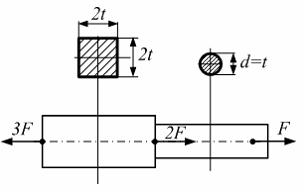
Ступенчатый стержень (см. рисунок) нагружен осевыми силами. Дано: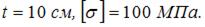 
Максимально допустимое значение параметра F равно ____ МН.
|
|
|
| 0,785
|
|
|
|
| 1,33
|
|
|
|
| 3,14
|
|
|
|
| 0,655
|
Решение:
Продольные силы на грузовых участках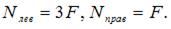 
Нормальные напряжения в поперечных сечениях грузовых участков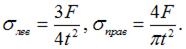 
Условие прочности для стержня имеет вид
откуда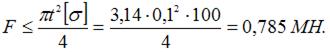 
ЗАДАНИЕ N 29 сообщить об ошибке
Тема: Напряжения в поперечном сечении стержня при плоском изгибе
Геометрическое место точек в поперечном сечении стержня при изгибе, в которых нормальные напряжения равны нулю, называется …
|
|
|
| нейтральной линией
|
|
|
|
| нейтральным слоем
|
|
|
|
| ядром сечения
|
|
|
|
| центром изгиба
|
Решение:
При изгибе стержня нормальные напряжения по высоте поперечного сечения изменяются по линейному закону. Геометрическое место точек в поперечном сечении, удовлетворяющее условию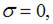 
называется нейтральной линией.
ЗАДАНИЕ N 30 сообщить об ошибке
Тема: Перемещения при изгибе. Расчет балок на жесткость
Консоль длиной 2 l нагружена двумя моментами. Жесткость поперечного сечения на изгиб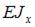 
по длине постоянна. Прогиб свободного конца консоли равен 
если значение момента М равно …
Решение:
Составим расчетную схему
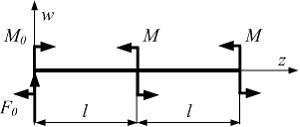
Воспользуемся универсальным уравнением упругой линии балки
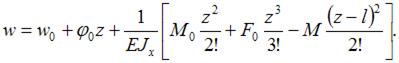
Из условий равновесия имеем
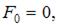
Прогиб и угол поворота в начале координат
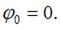
После преобразований найдем прогиб свободного конца консоли
Из условия 
получим 
ЗАДАНИЕ N 31 сообщить об ошибке
Тема: Расчет балок на прочность
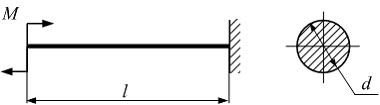
Консольная балка длиной l нагружена моментом М. Значение допускаемого нормального напряжения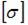 
известно. Из расчета на прочность по нормальные напряжениям минимально допустимое значение диаметра поперечного сечения d равно …
Решение:
Форма и размеры поперечного сечения по длине балки не меняются. Поэтому 
где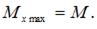 
Для круглого сечения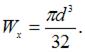 
Из условия прочности по нормальным напряжениям
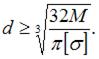
ЗАДАНИЕ N 32 сообщить об ошибке
Тема: Поперечная сила, изгибающий момент и их эпюры
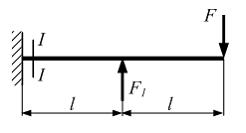
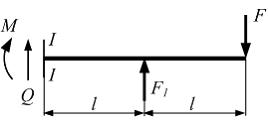
Консольная балка длиной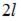 
нагружена силам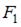и 
и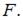 
Сечение I–I расположено бесконечно близко в заделке. Изгибающий момент в сечении I–I равен нулю, если значение силы 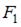равно …
Решение:
Рассекаем балку в сечении I–I на две части. Отбросим левую часть. Действие отброшенной левой части на оставшуюся заменяем поперечной силой Q и изгибающим моментом М.
Составим уравнение равновесия для определения изгибающего момента в сечении I–I
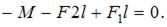
Из условия, что в данном сечении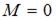 
, найдем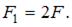 
ЗАДАНИЕ N 33 сообщить об ошибке
Тема: Формула Эйлера для критической силы сжатого стержня и пределы ее применимости
Наименьшему значению критической силы соответствует форма потери устойчивости, показанная на рисунке …
|
|
|
| а
|
|
|
|
| г
|
|
|
|
| б
|
|
|
|
| в
|
Решение:
Стержень, жестко защемленный одним концом и нагруженный осевой сжимающей силой на другом, находится в таких же условиях, как стержень шарнирно-закрепленный по обоим концам.
Поэтому, наименьшему значению критической силы соответствует форма потери устойчивости, показанная на рисунке «а».
ЗАДАНИЕ N 34 сообщить об ошибке
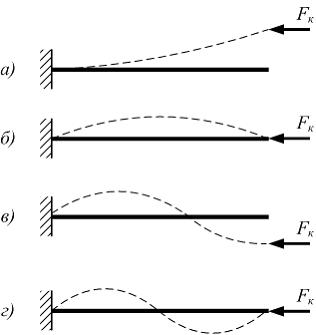
Тема: Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня
Стержень длиной l сжимается силой F. Напряжения в стержне не превышают предела пропорциональности. При уменьшении длины стержня в два раза, критическое напряжение ___ раза.
|
|
|
| увеличивается в 4
|
|
|
|
| увеличивается в 2
|
|
|
|
| уменьшается в 2
|
|
|
|
| уменьшается в 4
|
Решение:
Для определения критического напряжения, когда напряжения в стержне не превышают предела пропорциональности, воспользуемся формулой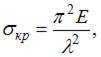 
где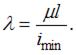 
При уменьшении длины стержня в два раза, при прочих равных условиях, гибкость стержня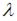 
уменьшается в два раза. Критическое напряжение увеличивается в четыре раза.
ЗАДАНИЕ N 35 сообщить об ошибке
Тема: Устойчивость за пределом пропорциональности. Расчет сжатых стержней на устойчивость
Стержень длиной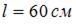 
, диаметром 
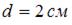сжимается силой F. Материал стержня – сталь 3 (
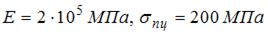). Схема закрепления показана на рисунке. Значение основного допускаемого напряжения 
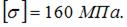Допускаемое значение силы F, которую можно безопасно приложить к стержню, равно ______ кН.
|
|
|
| 36,47
|
|
|
|
| 18,24
|
|
|
|
| 54,71
|
|
|
|
| 72,94
|
Решение:
Находим гибкость стержня по формул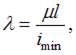е 
где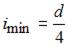 
, 
.
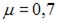После вычислений 
По таблице, зная марку материала и значение гибкости, находим, используя метод линейной интерполяции, значение коэффициента уменьшения основного допускаемого напряжения
, 
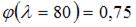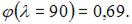
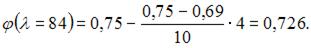
Допускаемое значение силы из расчета на устойчивость определим по формул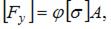е 
где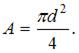 
После подстановки числовых значений получим
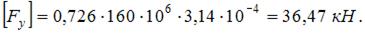
ЗАДАНИЕ N 36 сообщить об ошибке
Тема: Влияние условий закрепления концов стержня на величину критической силы
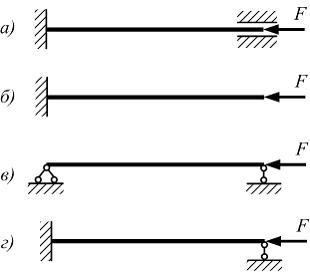
Стержни изготовлены из одного материала, имеют одинаковую длину, форму и размеры поперечного сечения. Схемы закрепления стержней, сжатых силой F, показаны на рисунке. Наименьшее значение гибкости имеет стержень, показанный на рисунке …
|
|
|
| а
|
|
|
|
| г
|
|
|
|
| в
|
|
|
|
| б
|
Решение:
Гибкость стержня определяется по формул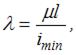е 
где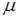 
– коэффициент приведения длины, который учитывает условия закрепления стержня. Наименьшее значение 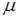имеем для схемы «а» 
Следовательно, гибкость будет наименьшей для стержня на схеме «а».
РАЗДЕЛ II. СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
