ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Прочность при ударных нагрузках
На раму постоянного квадратного поперечного сечения (см. рисунок) движется груз весом F со скоростью V.
Дано: 
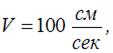
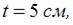
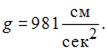
Величина динамического коэффициента, без учета массы рамы, равна …
|
|
| 37,7
|
|
|
|
| 26,7
|
|
|
|
| 3,19
|
|
|
|
| 52,8
|
Решение:
При горизонтальном ударе величина динамического коэффициента, без учета массы рамы, определяется по формуле
где 
– податливость рамы в направлении удара,
– кинетическая энергия груза,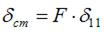 
– перемещение сечения, по которому производится удар, в направлении удара, вызванное силой F приложенной статически.
На рисунке показана схема нагружения рамы и эпюра изгибающего момента для определения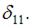 
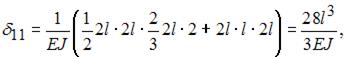
где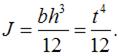 
После вычислений: 
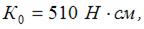
Подставляя значения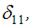 
в формулу динамического коэффициента, получаем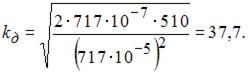 
ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Расчеты на прочность при напряжениях, периодически меняющихся во времени
Кривая усталости для незакаленных сталей имеет вид …
Решение:
Чем меньше напряжение, тем большее число циклов выдерживает образец не разрушаясь. При небольшом напряжении образец выдерживает неограниченно большое число циклов. Кривая усталости (кривая Велера) носит асимптотический характер.
ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Расчеты на прочность при колебаниях
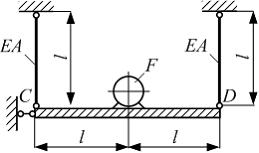
На абсолютно жесткий элемент CD, подвешенный на двух стержнях, установлен электродвигатель весом F, в котором имеется несбалансированная вращающаяся масса. Величины 
заданы. Выражение для числа оборотов в минуту электродвигателя, при котором наступает резонанс, имеет вид … Массу элемента CD и стержней в расчетах не учитывать.
Решение:
Условие резонанса 
где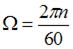 
– круговая частота изменений возмущающей силы, n – число оборотов в минуту ротора электродвигателя, 
– круговая частота собственных колебаний, 
– податливость системы, 
– масса электродвигателя.
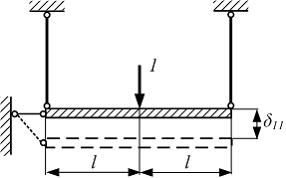
На рисунке показана схема нагружения для определения 
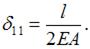
После соответствующих подстановок условие резонанса принимает вид
Откуда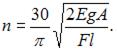 
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Деформированное состояние в точке. Связь между деформациями и напряжениями
На рисунке показан элементарный параллелепипед и вектора напряжений на его гранях. Линейные деформации: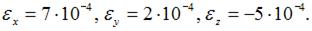 
После поворота элементарного параллелепипеда вместе с системой координат: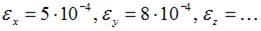 
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Напряженное состояние в точке. Главные площадки и главные напряжения)
На рисунке показан стержень, сжатый силами F. Главные напряжения в произвольной точке стержня: 
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Оценка прочности материала при сложном напряженном состоянии. Теории прочности
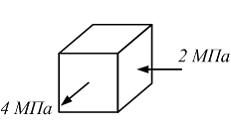
На рисунке показано напряженное состояние в точке. Материал хрупкий с пределом прочности на растяжение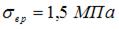 
и пределом прочности на сжатие 
Коэффициент Пуассона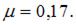 
Величина эквивалентного напряжения равна _____ МПа, прочность материала ______. Использовать теорию наибольших линейных деформаций удлинения.
|
|
|
| 4,34, не обеспечена
|
|
|
|
| 4,34, обеспечена
|
|
|
|
| 6, не обеспечена
|
|
|
|
| 3,66, обеспечена
|
Решение:
Главные напряжения: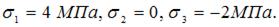 
Эквивалентное напряжение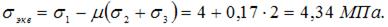 
Сравнивая величину эквивалентного напряжения с пределом прочности на растяжение, заключаем что прочность материала не обеспечена.
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Виды напряженного состояния
На рисунке показан элементарный параллелепипед и напряжения на его гранях 
Напряженное состояние элементарного параллелепипеда …
|
|
|
| плоское
|
|
|
|
| объемное
|
|
|
|
| плоское (чистый сдвиг)
|
|
|
|
| линейное (одноосное растяжение)
|
Решение:
Фронтальная грань элементарного параллелепипеда является главной площадкой с главным напряжением 
Два других главных напряжения определим по формуле 
Подставляя значения напряжений, получаем 
Присваивая главным напряжениям (с учетом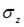 
) индексы 1, 2, 3, имеем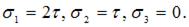 
Напряженное состояние плоское.
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Метод сил
Для статически неопределимой системы один из вариантов правильно выбранной основной системы показан на рисунке …
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Определение перемещений с помощью интегралов Мора. Правило Верещагина
Для определения перемещений в кривых плоских стержнях с помощью интегралов Мора, без учета влияния поперечных и продольных сил, используется формула 
Величина 
является …
|
|
|
| длиной элемента  оси стержня
|
|
|
|
| кривизной оси стержня
|
|
|
|
| радиусом кривизны оси стержня
|
|
|
|
| средней кривизной оси стержня
|
Решение:
Величина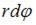 
(см. рисунок) является длиной элемента оси стержня.
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Расчет простейших статически неопределимых систем
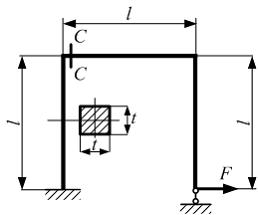
На рисунке показана рама с постоянным по контуру квадратным поперечным сечением, нагруженная силой F. Модуль упругости материала Е. Максимальное нормальное напряжение в сечении С-С рамы, вызванное изгибающим моментом, равно …
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Статическая неопределимость. Степень статической неопределенности
Степень статической неопределимости плоского замкнутого контура нагруженного силами, лежащими в его плоскости, равна …
|
|
|
| трем
|
|
|
|
| четырем
|
|
|
|
| шести
|
|
|
|
| двум
|
ЗАДАНИЕ N 13 сообщить об ошибке
Тема: Перемещение и деформация
До приложения к стержню сил F (см. рисунок) его длина равнялась 10 см. После приложения сил F длина стержня стала равна 9,95 см. Продольная линейная деформация стержня равна …
|
|
|
| 0,005
|
|
|
|
| 0,995
|
|
|
|
|
|
|
|
|
| 1,005
|
Решение:
Продольную линейную деформацию определим по формуле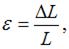 
где L – длина стержня до нагружения, 
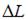– укорочение стержня. После подстановки числовых значений 
ЗАДАНИЕ N 14 сообщить об ошибке
Тема: Модели прочностной надежности
В курсе «Сопротивление материалов» все материалы, независимо от особенностей их микроструктуры, принято рассматривать как …
|
|
|
| сплошную среду
|
|
|
|
| атомную кристаллическую решетку
|
|
|
|
| совокупность хаотически расположенных кристаллов
|
|
|
|
| атомную кристаллическую решетку и совокупность хаотически расположенных кристаллов
|
Решение:
Модель сплошной среды не учитывает: местные пустоты, инородные включения в материале, особенности кристаллической решетки и пространственную ориентацию хаотически расположенных кристаллов, что позволяет широко использовать в сопротивлении материалов аппарат высшей математики и решать практические задачи.
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Внутренние силы и напряжения
При растяжении-сжатии прямого стержня дополнительные внутренние силы, действующие в поперечном сечении, образуют …
|
|
|
| пространственную систему параллельных сил перпендикулярных к плоскости сечения
|
|
|
|
| плоскую систему сходящихся сил
|
|
|
|
| плоскую систему параллельных сил
|
|
|
|
| пространственную систему сходящихся сил
|
Решение:
При растяжении-сжатии прямого стержня дополнительные внутренние силы, действующие в поперечном сечении, образуют пространственную систему параллельных сил перпендикулярных к плоскости сечения.
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Основные понятия, определения, допущения и принципы
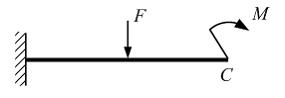
Прогиб сечения С равен сумме прогибов, вызванных силой F и моментом М, приложенных по отдельности. Данное утверждение записано на основании принципа …
|
|
|
| независимости действия сил (принципа суперпозиции)
|
|
|
|
| Сен-Венана
|
|
|
|
| малых перемещений
|
|
|
|
| возможных перемещений
|
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Расчет на прочность при кручении
Стержень круглого поперечного сечения из пластичного материала работает на кручение. При расчете по допускаемым касательным напряжениям за предельное напряжение принимается …
|
|
|
| предел текучести при чистом сдвиге
|
|
|
|
| предел текучести при растяжении
|
|
|
|
| предел прочности при чистом сдвиге
|
|
|
|
| предел упругости при чистом сдвиге
|
Решение:
Предел текучести при чистом сдвиге считается предельным напряжением в расчетах по допускаемым напряжениям стержней из пластичного материала, работающих на кручение.
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Крутящий момент. Деформации и напряжения
На рисунке показан стержень, работающий на кручение. Крутящий момент на среднем грузовом участке равен …
ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Чистый сдвиг. Расчет на сдвиг (срез)
Напряженное состояние «чистый сдвиг» показано на рисунке. Штриховыми линиями показан характер деформации. Углом сдвига называется угол …
Решение:
Отрезок ВС называется абсолютным сдвигом. Отношение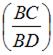 
называется относительным сдвигом или углом сдвига.
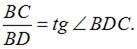При малых перемещениях 
– угол сдвига.
ЗАДАНИЕ N 20 сообщить об ошибке
Тема: Расчет на жесткость при кручении
Размерность относительного угла закручивания …
0, 0
