Решение:
Главные напряжения: 
Эквивалентное напряжение 
Коэффициент запаса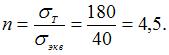 
Для перехода материала из упругого состояния в пластичное напряжения 
следует увеличить в 4,5 раза.
ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Виды напряженного состояния
Число типов (классов) напряженных состояний в точке равно …
|
|
| трем
|
|
|
|
| двум
|
|
|
|
| четырем
|
|
|
|
| шести
|
Решение:
Напряженные состояния в точке деляется на три типа (линейное, плоское и объемное).
ЗАДАНИЕ N 20 сообщить об ошибке
Тема: Деформированное состояние в точке. Связь между деформациями и напряжениями
На рисунке показано напряженное состояние в точке. Модуль упругости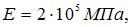 
коэффициент Пуассона 
Относительное изменение объема равно …
ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Расчеты на прочность при напряжениях, периодически меняющихся во времени
Линейная протяженность очага концентрации напряжений (см. рисунок) равна …
|
|
|
| 2 b
|
|
|
|
| H
|
|
|
|
| 2 h
|
|
|
|
| b
|
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Расчеты на прочность с учетом сил инерции
Стержень ВС длиной l, площадью поперечного сечения А равномерно вращается с постоянной угловой скоростью 
вокруг вертикальной оси. Удельный вес материала 
(вес единицы объема) задан. Значение максимального нормального напряжения в стержне равно …
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Прочность при ударных нагрузках
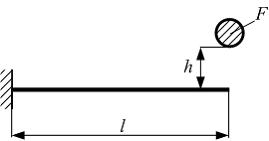
Груз весом F падает на балку с высоты h. Модуль упругости материала балки Е задан. При повороте поперечного сечения из положения а в положение б максимальные динамические напряжения …
Динамический коэффициент определять по приближенной формуле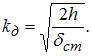 
|
|
|
| не изменяются
|
|
|
|
| увеличиваются в два раза
|
|
|
|
| уменьшаются в два раза
|
|
|
|
| увеличиваются в три раза
|
ЗАДАНИЕ N 24 сообщить об ошибке
Тема: Расчеты на прочность при колебаниях
На балку установлен электродвигатель (см. рисунок) весом 
в котором имеется несбалансированная вращающаяся масса. Длина балки 
поперечное сечение состоит из двух швеллеров №8 с общим моментом сопротивления 
Круговая частота изменений возмущающей силы 
круговая частота собственных колебаний 
максимальное значение возмущающей силы 
заданы. Массу балки в расчетах не учитывать.
Среднее напряжение и амплитуда цикла нормальных напряжений в самых напряженных точках балки: 
|
|
|
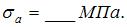
| 15; 13
|
|
|
|
| 20; 16
|
|
|
|
| 13; 11
|
|
|
|
| 23; 18
|
Решение:
Максимальное нормальное напряжение в среднем сечении балки от веса электродвигателя (среднее напряжение)
Максимальное нормальное напряжение в среднем сечении балки от наибольшей величины возмущающей силы, приложенной статически
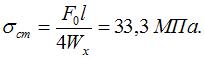
Динамический коэффициент
Амплитуда цикла нормальных напряжений в самых напряженных точках среднего сечения
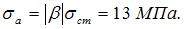
ЗАДАНИЕ N 25 сообщить об ошибке
Тема: Расчет на жесткость при кручении
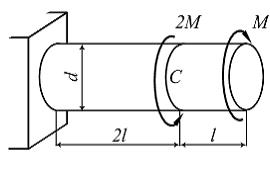
Стержень, показанный на рисунке, испытывает деформацию кручение. Известны величины: М, l, 
– допустимый угол поворота поперечного сечения С в радианах, G – модуль сдвига материала стержня. Минимально допустимое значение диаметра d равно …
Решение:
Крутящий момент на левом грузовом участке стержня по модулю равен М.
Условие жесткости имеет вид 
где 
– длина левого грузового участка.
Подставляя значение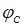 
в условие жесткости, получаем 
откуда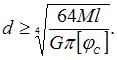 
ЗАДАНИЕ N 26 сообщить об ошибке
Тема: Чистый сдвиг. Расчет на сдвиг (срез)
На рисунке показано клеевое соединение втулки с валом, передающее крутящий момент. Задано: М, d, l, 
– допускаемое касательное напряжение на срез клеевого слоя. Условие прочности на срез клеевого слоя имеет вид …
Решение:
Срез клеевого слоя происходит по цилиндрической поверхности диаметром d и длиной l (см. рисунок). Считаем, что касательные напряжения распределены по площади среза равномерно. Запишем уравнение равновесия 
откуда 
Условие прочности на срез клеевого слоя имеет вид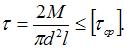 
ЗАДАНИЕ N 27 сообщить об ошибке
Тема: Расчет на прочность при кручении
На рисунке показана труба, работающая на кручение. Заданы величины: 
предел текучести при чистом сдвиге 
Фактический коэффициент запаса из расчета по текучести в самых напряженным точках равен …
|
|
|
| 2,1
|
|
|
|
| 1,2
|
|
|
|
| 3,1
|
|
|
|
| 2,5
|
ЗАДАНИЕ N 28 сообщить об ошибке
Тема: Крутящий момент. Деформации и напряжения
На рисунке показан стержень, работающий на кручение. Максимальные касательные напряжения в поперечном сечении стержня равны …
ЗАДАНИЕ N 29 сообщить об ошибке
Тема: Перемещения при изгибе. Расчет балок на жесткость
На рисунке показан примерный вид изогнутой оси балки. Схема нагружения балки, соответствующая представленной форме изгиба, показана на схеме …
|
|
|
| г
|
|
|
|
| а
|
|
|
|
| в
|
|
|
|
| б
|
ЗАДАНИЕ N 30 сообщить об ошибке
Тема: Поперечная сила, изгибающий момент и их эпюры
На схеме показана отсеченная часть балки и нагрузка, действующая на нее. Неверным является утверждение, что изгибающий момент …
|
|
|
| на участке ВС постоянный
|
|
|
|
| на участке АВ меняется по закону квадратной параболы
|
|
|
|
| в сечении А имеет экстремальное значение
|
|
|
|
| на участке СD переменный
|
Решение:
Из дифференциальных зависимостей при изгибе 
следует, что на участке, где 
, поперечная сила постоянна, а изгибающий момент меняется по линейному закону. Поэтому утверждение, что изгибающий момент на участке ВС постоянный является неверным.
ЗАДАНИЕ N 31 сообщить об ошибке
Тема: Расчет балок на прочность
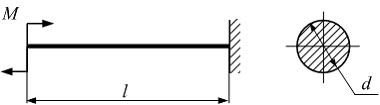
Консольная балка длиной l нагружена моментом М. Значение допускаемого нормального напряжения 
известно. Из расчета на прочность по нормальные напряжениям минимально допустимое значение диаметра поперечного сечения d равно …
Решение:
Форма и размеры поперечного сечения по длине балки не меняются. Поэтому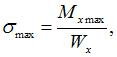 
где 
Для круглого сечения 
Из условия прочности по нормальным напряжениям
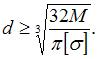
ЗАДАНИЕ N 32 сообщить об ошибке
Тема: Напряжения в поперечном сечении стержня при плоском изгибе
Для определения касательных напряжений в точках поперечного сечения балки, при плоском поперечном изгибе, используют формулу …
Решение:
Касательные напряжения в точках поперечного сечения балки при плоском поперечном изгибе определяют по формуле Журавского
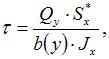
где 
– значение поперечной силы в данном сечении; 
– статический момент относительно нейтральной линии площади сечения расположенной выше (или ниже) точки К в которой определяется касательное напряжение линии (см. рисунок, заштрихованная площадь); 
– ширина поперечного сечения; 
– осевой момент инерции сечения относительно главной центральной оси (нейтральной линии).
ЗАДАНИЕ N 33 сообщить об ошибке
Тема: Метод сил
Результат умножения симметричной эпюры на кососимметричную – …
|
|
|
| ноль
|
|
|
|
| положительное число
|
|
|
|
| отрицательное число
|
|
|
|
| число положительное и отрицательно
|
Решение:
На рисунке показаны симметричная и кососимметричная эпюры. Буквами 
и 
обозначены центры тяжестей площадей 
и 
Перемножим площади 
на ординаты 
и сложим произведения. Получим нулевой результат.
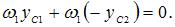
ЗАДАНИЕ N 34 сообщить об ошибке
Тема: Определение перемещений с помощью интегралов Мора. Правило Верещагина
Формула интеграла Мора, не учитывающая влияние поперечной силы, для данной расчетной схемы имеет вид …
ЗАДАНИЕ N 35 сообщить об ошибке
Тема: Расчет простейших статически неопределимых систем
На рисунке показана балка круглого поперечного сечения нагруженная моментом М. Известны величины: М, Е, d, l.
Максимальное нормальное напряжение в поперечном сечении балки, по абсолютной величине, равно …
ЗАДАНИЕ N 36 сообщить об ошибке
Тема: Статическая неопределимость. Степень статической неопределенности
Связи, обеспечивающие кинематическую неизменяемость системы, называются …
|
|
|
| необходимыми
|
|
|
|
| дополнительными (линейными)
|
|
|
|
| абсолютно жесткими
|
|
|
|
| упругими
|
Преподаватель: Секретов М.В.
Специальность: 150400.62 - Технологические машины и оборудование
Группа: ГМО-09
Дисциплина: Сопротивление материалов
Идентификатор студента: Ичин-Норбу И.У.
Логин: 06ps776352
Начало тестирования: 2012-12-12 13:47:49
Завершение тестирования: 2012-12-12 14:12:30
Продолжительность тестирования: 24 мин.
Заданий в тесте: 36
Кол-во правильно выполненных заданий: 14
Процент правильно выполненных заданий: 38 %
ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Влияние условий закрепления концов стержня на величину критической силы
Выражение 
определяет критическую силу сжатого стержня …
|
|
|
| с шарнирно-опертыми концами
|
|
|
|
| при любых условиях закрепления
|
|
|
|
| шарнирно-опертого при наличии промежуточной опоры
|
|
|
|
| с одним защемленным концом и свободным другим
|
Решение:
Формула Эйлера для определения наименьшего значения критической силы имеет вид 
Коэффициент приведения длины 
зависит от условий закрепления стержня. Для стержня с шарнирно-опертыми концами 
Поэтому выражение определяет критическую силу для сжатого стержня с шарнирно-опертыми концами.
