Решение:
Балка (рис. 1) один раз статически неопределима. Для раскрытия статической неопределимости используем метод сил. На рисунках 2 и 3 показана основная и эквивалентная системы.
Каноническое уравнение метода сил имеет вид 
Определяем коэффициенты канонического уравнение, используя для вычисления интегралов Мора способ Верещагина. Для этого строим эпюры изгибающих моментов в грузовом и единичном состояниях основной системы (рис. 4, 5) и перемножаем их.
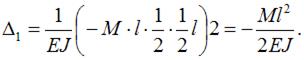
Подставляя значения 
и 
в каноническое уравнение, получаем 
Откуда 
Подставляем значение 
в эквивалентную систему (рис. 6) и строим окончательную эпюру изгибающего момента (рис. 7).
ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Метод сил
Симметричными внутренними силовыми факторами являются …
|
|
| изгибающие моменты и продольная сила
|
|
|
|
| крутящий момент и продольная сила
|
|
|
|
| продольная и поперечные силы
|
|
|
|
| поперечные силы и крутящий момент
|
Решение:
На рисунке показан стержень, рассеченный поперечным сечением, и внутренние силовые факторы. Симметричными внутренними силовыми факторами являются изгибающие моменты 
и 
и продольная сила N.
ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Определение перемещений с помощью интегралов Мора. Правило Верещагина
Формула интеграла Мора, не учитывающая влияние поперечной силы, для данной расчетной схемы имеет вид …
Решение:
На всех участках рамы нулю не равняется изгибающий момент и поперечная сила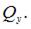 
Кроме того на II и III участках нулю не равняется крутящий момент 
По условию задачи влияние поперечной силы на перемещения не учитывается. Следовательно, формула интеграла Мора для данной расчетной схемы имеет вид 
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Механические свойства и механические характеристики материалов
Коэффициент Пуассона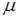 
для изотропного материала изменяется в пределах …
Решение:
Область изменения коэффициента Пуассона изотропного материала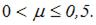 
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Испытание конструкционных материалов на растяжение и сжатие
Цилиндрический образец при испытании на сжатие принимает бочкообразную форму вследствие …
|
|
|
| сил трения между торцевыми поверхностями образца и поверхностями плит испытательной машины
|
|
|
|
| наличия пустот и микротрещин в материале образца
|
|
|
|
| резкого увеличения поперечной деформации образца в средней части образца
|
|
|
|
| несовершенства начальной геометрической формы образца
|
Решение:
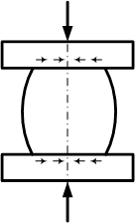
Бочкообразная форма образца объясняется наличием сил трения между поверхностями плит испытательной машины и торцевыми поверхностями образца. Силы трения препятствует поперечной деформации материала. По мере удаления от торцов влияние сил трения уменьшается.
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Продольная сила. Напряжения и деформации
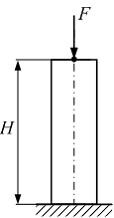
Колонна высотой H (см. рисунок) находится под действием собственного веса и силы F. Удельный вес материала колонны 
(вес единицы объема), площадь поперечного сечения А – известны. Максимальные нормальные напряжения в поперечном сечении колонны равны …
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Расчеты стержней на прочность и жесткость
Абсолютно жесткий элемент СК подвешен на двух стержнях и нагружен силой F (см. рисунок). Известны величины: сила F, линейный размер l,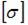 
– допускаемое напряжение для материала стержней. Вес элемента СК в расчетах не учитывается. Минимально допустимые размеры поперечных сечений стержней имеют значения: d = ___, t = ___.
Решение:
Рассмотрим равновесие элемента СК (см. рисунок). Уравнения равновесия имеют вид:
откуда 
Условия прочности для стержней:
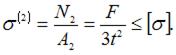
Следовательно,
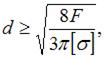
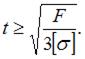
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Напряжения в поперечном сечении стержня при плоском изгибе
На консольную ступенчатую балку длиной 
действует равномерно распределенная нагрузка интенсивности q. Поперечное сечение левой ступени – квадрат с размерами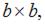 
правая – имеет прямоугольное сечение с размерами 
и 
. Максимальное значение нормального напряжения в балке равно …
(Концентрацию напряжений не учитывать).
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Поперечная сила, изгибающий момент и их эпюры
Эпюра изгибающих моментов показана на рисунке. Неверным является утверждение, что поперечная сила …
|
|
|
| в сечении В не равна нулю
|
|
|
|
| на участке АС переменна
|
|
|
|
| на участке CD постоянна
|
|
|
|
| в сечении С изменяется скачком
|
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Перемещения при изгибе. Расчет балок на жесткость
Консольная балка длиной 
нагружена моментом 
Поперечное сечение балки прямоугольник: 
Модуль упругости материала 
Радиус кривизны балки в сечении I–I равен ___ (м).
|
|
|
| 3,6
|
|
|
|
|
|
|
|
|
| 5,2
|
|
|
|
| 4,8
|
Решение:
Балка испытывает чистый изгиб. Значение изгибающего момента в любом сечении 
Следовательно, балка изгибается по окружности. Для определения радиуса кривизны воспользуемся формулой
, откуда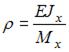 
.
– жесткость поперечного сечения балки на изгиб. Осевой момент инерции сечения 
.
После вычислений найдем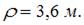 
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Расчет балок на прочность
Консольная балка прямоугольного сечения с размерами b и 2 b нагружена равномерно распределенной нагрузкой. Допускаемое нормальное напряжение для материала балки 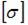задано. Из расчета на прочность по нормальным напряжениям максимально допустимое значение интенсивности нагрузки q равно …
Решение:
Форма и размеры поперечного сечения балки по длине не меняются. поэтому, максимальное нормальное напряжение определим по формуле
Учитывая, что
найдем 
Из условия прочности по допускаемым нормальным напряжениям
.
получим
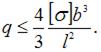
ЗАДАНИЕ N 13 сообщить об ошибке
Тема: Основные понятия, определения, допущения и принципы
На рисунке показаны два стержня с одинаковой площадью поперечного сечения, работающие на растяжение. Нормальные напряжения в сечениях обоих стержней, достаточно удаленных от мест приложения сил, равны согласно …
|
|
|
| принципу Сен-Венана
|
|
|
|
| принципу суперпозиции
|
|
|
|
| принципу начальных размеров
|
|
|
|
| гипотезе сплошной среды
|
Решение:
Системы сил, растягивающие стержни, статически эквивалентны и приложены к малой площади поверхности стержня. Поэтому нормальные напряжения в сечениях стержней, удаленных от мест приложения сил, равны согласно принципу Сен-Венана.
ЗАДАНИЕ N 14 сообщить об ошибке
Тема: Модели прочностной надежности
В курсе «Сопротивление материалов» все материалы, независимо от особенностей их микроструктуры, принято рассматривать как …
|
|
|
| сплошную среду
|
|
|
|
| атомную кристаллическую решетку
|
|
|
|
| совокупность хаотически расположенных кристаллов
|
|
|
|
| атомную кристаллическую решетку и совокупность хаотически расположенных кристаллов
|
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Внутренние силы и напряжения
В процессе нагружения тела внешними силами между частицами материала возникают дополнительные внутренние силы, которые …
|
|
|
| являются предметом изучения в сопротивлении материалов
|
|
|
|
| не являются предметом изучения в сопротивлении материалов
|
|
|
|
| являются предметом изучения в сопротивлении материалов при небольших внешних нагрузках
|
|
|
|
| не являются предметом изучения в сопротивлении материалов, если тело находится в покое
|
Решение:
Дополнительные внутренние силы, возникающие между частицами материала, в процессе нагружения тела внешней нагрузкой являются предметом изучения в сопротивлении материалов.
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Перемещение и деформация
Угловая деформация − это …
|
|
|
| изменение угла между двумя взаимно перпендикулярными до деформации малыми отрезками, проходящими через данную точку.
|
|
|
|
| угол поворота прямого отрезка малой длины в пространстве
|
|
|
|
| сумма углов поворота прямого отрезка малой длины в координатных плоскостях 
|
|
|
|
| угол поворота тела в пространстве как жесткого целого
|
Решение:
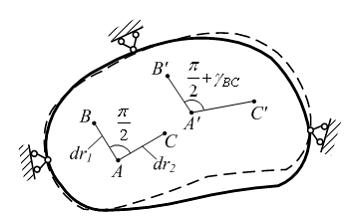
Рассмотрим два взаимно перпендикулярных до деформации малых отрезка 
и 
(см. рисунок). В процессе деформации тела точки А, В, С, перемещаются в положения А', В', С '. Прямой угол между направлениями АВ и АС изменяется на величину 
Изменение прямого угла между направлениями АВ и АС называется угловой деформацией или углом сдвига между этими направлениями. Если рассматривать различные пары взаимно перпендикулярных до деформации направлений, проходящих через точку А, то угловые деформации между ними в общем случае будут различными.
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Изгиб с растяжением?сжатием
Сила приложена в центре тяжести поперечного сечения по направлению оси стержня. При перемещении силы от центра тяжести, параллельно начальному положению, нормальное напряжение в центре тяжести поперечного сечения …
|
|
|
| остается неизменным
|
|
|
|
| увеличивается пропорционально расстоянию, на которое переносится сила
|
|
|
|
| уменьшается пропорционально расстоянию, на которое переносится сила
|
|
|
|
| увеличивается, когда сила выйдет за границу ядра сечения
|
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Изгиб с кручением
Стержень прямоугольного сечения с размерами b и 2 b нагружен силой F. Опасными являются точки …
|
|
|
| С и М
|
|
|
|
| B и D
|
|
|
|
| A и K
|
|
|
|
| A и B
|
Решение:
В сечении стержня, расположенном бесконечно близко к заделке возникают изгибающий момент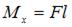 
и крутящий момент 
От изгибающего момента максимальные нормальные напряжения, равные по абсолютной величине, возникают в точках наиболее удаленных от главной центральной оси x. На линии BD имеем растягивающие напряжения, на линии АК – сжимающие.
Максимальные касательные напряжения, при кручении стержня с прямоугольным сечением, возникают в середине длинной стороны прямоугольника. Поэтому, опасными будут точки С и М.
ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Пространственный и косой изгиб
В поперечном прямоугольном сечении стержня с размерами b и 2 b определены значения изгибающих моментов 
и 
Нормальное напряжение в точке В равно …
Решение:
Изгибающий момент вызывает растяжение верхней половины сечения, сжатие – нижней. Момент правую половину сечения растягивает, левую – сжимает.
Используя формулу для определения нормальных напряжений при косом изгибе, найдем
где координаты точки В, в системе главных центральных осей 
взяты по абсолютной величине.
