ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Перемещение и деформация
В процессе деформации точки А, В, С деформируемого тела перемещаются в плоскости xoy и занимают положения 
. Прямолинейные отрезки АВ и АС поворачиваются на углы 
и 
Угловая деформация в точке А между направлениями АВ и АС, когда длины отрезков стремятся к нулю, равна …
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Оценка прочности материала при сложном напряженном состоянии. Теории прочности
На рисунке показано напряженное состояние элементарного объема из материла, у которого предел прочности на растяжение в два раза меньше предела прочности на сжатие. Определите величину эквивалентного напряжения и оцените прочность материала, используя теорию прочности О. Мора. Величина эквивалентного напряжения равна ___ МПа, прочность материала …
|
|
|
| 1,25, обеспечена
|
|
|
|
| 1, обеспечена
|
|
|
|
| 1,75, не обеспечена
|
|
|
|
| 2, не обеспечена
|
Решение:
В данном случае на чистый сдвиг накладывается одноосное растяжение. Известно, что при чистом сдвиге 
а 
Третье главное напряжение равно 
Присваивая главным напряжением индексы, получаем 
Эквивалентное напряжение определяем по формуле 
После подстановки 
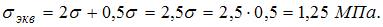Сравнивая 
с 
, заключаем, что прочность данного материала при заданном напряженном состоянии обеспечена.
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Напряженное состояние в точке. Главные площадки и главные напряжения)
Нормальные напряжения, действующие на главных площадках, называются …
|
|
|
| главными напряжениями
|
|
|
|
| экстремальными напряжениями
|
|
|
|
| октаэдрическими напряжениями
|
|
|
|
| инвариантами напряженного состояния
|
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Виды напряженного состояния
Напряженное состояние элементарного объема является – …
|
|
|
| объемное
|
|
|
|
| плоское
|
|
|
|
| линейное (одноосное растяжение)
|
|
|
|
| линейное (одноосное сжатие)
|
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Деформированное состояние в точке. Связь между деформациями и напряжениями
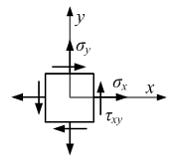
Если величины: 
то напряжения: 
|
|
|
| 286, 286, 80
|
|
|
|
| 182, 182, 60
|
|
|
|
| 250, 250, 70
|
|
|
|
| 123, 123, 50
|
Решение:
Запишем обобщенный закон Гука для плоского напряженного состояния 
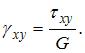
Решая эту систему уравнений относительно 
получаем 
Подставляя в эти формулы численные значения, получим:
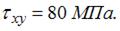
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Испытание конструкционных материалов на растяжение и сжатие
При испытании образца на растяжение силами F (см. рисунок) стрелка тензометра А с базой, равной 60 мм, переместилась с деления 5 на деление 9. Цена деления шкалы тензометра 0,001 мм. Модуль упругости материала образца 
Напряжение в крайнем правом слое равно ____ МПа.
|
|
|
| 13,3
|
|
|
|
|
|
|
|
|
| 46,7
|
|
|
|
|
|
Решение:
Напряжение определим по закону Гука.
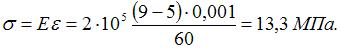
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Расчеты стержней на прочность и жесткость
Элемент КСD закреплен с помощью шарнирно неподвижной опоры и стержняс жесткостью поперечного сечения на растяжение ЕА (см. рисунок). Система нагружена равномерно распределенной нагрузкой с интенсивностью q. Допустимая величина удлинения стержня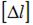 
задана.Условие жесткости имеет вид …
Решение:
Рассмотрим равновесие элемента КСD и определим продольную силу в стержне 
Удлинение стержня 
а условие жесткости имеет вид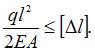 
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Продольная сила. Напряжения и деформации
Стержень длиной l (см. рисунок) находится под действием собственного веса. Вес стержня Q, площадь поперечного сечения А, модуль упругости материала стержня Е – известны. Продольная линейная деформация в среднем сечении стержня равна …
Решение:
Продольную линейную деформацию в среднем сечении стержня определим по формуле 
где 
– нормальное напряжение в среднем сечении. Подставляя выражение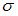 
в формулу для 
получим 
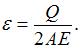
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Механические свойства и механические характеристики материалов
Материал, механические характеристики которого не зависят от направления, называется …
|
|
|
| изотропным
|
|
|
|
| однородным
|
|
|
|
| сплошным
|
|
|
|
| анизотропным
|
ЗАДАНИЕ N 13 сообщить об ошибке
Тема: Влияние условий закрепления концов стержня на величину критической силы
Схема закрепления стержня длиной l показана на рисунке. При удалении промежуточной опоры в середине пролета значение критического напряжения … При решении учитывать, что напряжения в сжатых стержнях не превышают предел пропорциональности.
|
|
|
| уменьшится в 4 раза
|
|
|
|
| не изменится
|
|
|
|
| увеличится в 4 раза
|
|
|
|
| уменьшится в 2 раза
|
Решение:
Для определения критического напряжения, когда напряжения в сжатом стержне не превышают предел пропорциональности, используем формулу
где 
Коэффициент приведения длины 
учитывает условия закрепления стержня. До удаления опоры 
после удаления – 
Следовательно, значение критического напряжения после удаления опоры, уменьшится в четыре раза.
ЗАДАНИЕ N 14 сообщить об ошибке
Тема: Формула Эйлера для критической силы сжатого стержня и пределы ее применимости
Для стержня с шарнирно-опертыми концами значению критической силы 
соответствует изгиб стержня по …
|
|
|
| полуволне синусоиды
|
|
|
|
| квадратичной параболе
|
|
|
|
| дуге окружности
|
|
|
|
| синусоиде
|
Решение:
При выводе формулы Эйлера пользуются приближенным дифференциальным уравнением изогнутой оси стержня. После интегрирования и выполнения граничных условий получают наименьшее значение критической силы 
и форму изогнутой оси стержня в виде полуволны синусоиды 
с максимальным прогибом А.
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня
Стержень квадратного сечения с размерами 
, длиной l сжимается силами F. При увеличении каждой стороны квадрата в два раза, при прочих равных условиях, гибкость стержня ___ раза.
|
|
|
| уменьшится в 2
|
|
|
|
| увеличится в 4
|
|
|
|
| уменьшится в 4
|
|
|
|
| увеличится в 2
|
Решение:
Гибкость стержня определяется по формуле 
При увеличении размеров поперечного сечения, при прочих равных условиях, гибкость будет зависеть от минимального радиуса поперечного сечения 
В первом варианте 
во втором –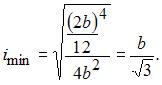 
Следовательно, во втором варианте гибкость стержня уменьшится в два раза.
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Устойчивость за пределом пропорциональности. Расчет сжатых стержней на устойчивость
Стержень изготовлен из стали с характеристиками: предел пропорциональности 
модуль упругости 
Формула Эйлера для определения критической силы сжатого стержня изготовленного из данного материала применима, если гибкость стержня …
Решение:
Формула Эйлера для определения критической силы сжатого стержня применима, когда
или
Значит, формула Эйлера становится непригодной при гибкости стержня, меньшей предельного значения.
В рассматриваемом случае
.
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Определение перемещений с помощью интегралов Мора. Правило Верещагина
Для определения перемещений в кривых плоских стержнях с помощью интегралов Мора, без учета влияния поперечных и продольных сил, используется формула 
Величина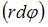 
является …
|
|
|
| длиной элемента  оси стержня
|
|
|
|
| кривизной оси стержня
|
|
|
|
| радиусом кривизны оси стержня
|
|
|
|
| средней кривизной оси стержня
|
Решение:
Величина 
(см. рисунок) является длиной элемента оси стержня.
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Статическая неопределимость. Степень статической неопределенности
Два раза статически неопределимая система показана на рисунках …
|
|
|
| 1, 4
|
|
|
|
| 1, 3
|
|
|
|
| 2, 3
|
|
|
|
| 3, 4
|
Решение:
На рисунках 2 и 3 показаны один раз статически неопределимые системы. Два раза статически неопределимая система показана на рисунках 1 и 4.
ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Расчет простейших статически неопределимых систем
На рисунке показана балка круглого поперечного сечения нагруженная моментом М. Известны величины: М, Е, d, l.
Максимальное нормальное напряжение в поперечном сечении балки, по абсолютной величине, равно …
ЗАДАНИЕ N 20 сообщить об ошибке
Тема: Метод сил
Число дополнительных связей, от которых необходимо освободить систему, при раскрытии статической неопределимости методом сил равно …
Решение:
Система четыре раза статически неопределима (один раз внешним образом и три раза внутренним), то есть имеет четыре дополнительные связи. Поэтому при выборе основной системы необходимо ее освободить от четырех дополнительных связей.
ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Перемещения при изгибе. Расчет балок на жесткость
Однопролетная балка длиной l, высотой h нагружена равномерно распределенной нагрузкой. Радиус кривизны нейтрального слоя балки в середине пролета равен 
. Жесткость поперечного сечения на изгиб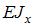 
по всей длине постоянна. Максимальное нормальное напряжение в балке равно … (Влияние поперечной силы на изменение кривизны не учитывать).
Решение:
При изгибе балки кривизна нейтрального слоя связана с изгибающим моментом и жесткостью поперечного сечения на изгиб соотношением 
Следовательно, в середине пролета, в котором возникает максимальный изгибающий момент, имеем 
Максимальное нормальное напряжение найдем по формуле 
Учитывая, что 
, получим 
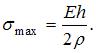
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Расчет балок на прочность
При расчете балки на прочность по касательным напряжениям, когда форма и размеры поперечного сечения по длине не меняются, опасным считается сечение …
