РАЗДЕЛ II. СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ 4 страница

ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Механические свойства и механические характеристики материалов

При нагружении образца прямоугольного сечения силами стрелки тензометров А и В переместились на 6 и 4 деления соответственно. Базы тензометров – 20 мм. Цена деления шкалы тензометров – 0,001 мм. Модуль упругости материала образца равен ____ МПа.

 

ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Продольная сила. Напряжения и деформации
Продольная сила есть равнодействующая …

			нормальных напряжений в поперечном сечении стержня
			внешних сил, приложенных к отсеченной части стержня
			нормальных напряжений и внешних сил, приложенных к отсеченной части стержня
			всех внешних сил, приложенных к стержню

 

ЗАДАНИЕ N 24 сообщить об ошибке
Тема: Расчеты стержней на прочность и жесткость

Известны величины: (см. рисунок). Зазор полностью перекрывается, когда сила F становится равной …

 

Решение:
Когда зазор полностью перекрывается, перемещение сечения С стержня становится равным величине зазора. откуда

 

ЗАДАНИЕ N 25 сообщить об ошибке
Тема: Деформированное состояние в точке. Связь между деформациями и напряжениями
Для изотропного материала главные оси деформированного состояния совпадают с …

			главными осями напряженного состояния
			главными центральными осями поперечного сечения
			осями симметрии кристаллической решетки
			ребрами элементарного объема

 

ЗАДАНИЕ N 26 сообщить об ошибке
Тема: Оценка прочности материала при сложном напряженном состоянии. Теории прочности

На рисунке показано напряженное состояние в точке. Материал пластичный с пределом текучести Коэффициент запаса по теории наибольших касательных напряжений равен …

			2,2
			6,7
			3,3
			1,5

 

Решение:
Главные напряжения:
Эквивалентное напряжение по теории наибольших касательных напряжений
Коэффициент запаса

 

ЗАДАНИЕ N 27 сообщить об ошибке
Тема: Виды напряженного состояния
Тип напряженного состояния в точке тела, нагруженного произвольной системой сил, устанавливается по …

			количеству главных напряжений не равных нулю
			значениям главных напряжений не равных нулю
			известным механическим характеристикам материала
			характеру внешней нагрузки

 

Решение:
Тип напряженного состояния в точке тела, нагруженного произвольной системой сил, устанавливается по числу главных напряжений не равных нулю.
Одно из главных напряжений не равно нулю – напряженное состояние линейное.
Два главных напряжения не равны нулю – напряженное состояние плоское.
Все три главных напряжения не равны нулю – напряженное состояние объемное.

 

ЗАДАНИЕ N 28 сообщить об ошибке
Тема: Напряженное состояние в точке. Главные площадки и главные напряжения)
Число компонент напряженного состояния, полностью определяющих напряженное состояние в точке, равно …

			шести
			девяти
			четырем
			двум

 

Решение:
Шесть компонент напряженного состояния: полностью определяют напряженное состояние в точке.

 

ЗАДАНИЕ N 29 сообщить об ошибке
Тема: Изгиб с растяжением?сжатием
Сила приложена в центре тяжести поперечного сечения по направлению оси стержня. При перемещении силы от центра тяжести, параллельно начальному положению, нормальное напряжение в центре тяжести поперечного сечения …

			остается неизменным
			увеличивается пропорционально расстоянию, на которое переносится сила
			уменьшается пропорционально расстоянию, на которое переносится сила
			увеличивается, когда сила выйдет за границу ядра сечения

 

Решение:
При перемещении силы от центра тяжести сечения стержень испытывает внецентренное растяжение (сжатие). Нормальное напряжение в произвольной точке поперечного сечения определяется по формуле
где x, y – координаты точки в системе главных центральных осей, взятые по абсолютной величине.
В центре тяжести поперечного сечения
Следовательно, нормальное напряжение в центре тяжести сечения, при перемещении силы от центра тяжести сечения остаются неизменными.

 

ЗАДАНИЕ N 30 сообщить об ошибке
Тема: Изгиб с кручением
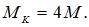В поперечном сечении стержня действуют изгибающие моменты и крутящий момент Сечение круглое диаметром d. Значение эквивалентного напряжения в опасной точке, по теории удельной потенциальной энергии формоизменения, равно …

 

Решение:
Согласно теории удельной потенциальной энергии формоизменения эквивалентное напряжение в опасной точке круглого сечения при изгибе с кручением определяется по формуле
где – момент сопротивления при изгибе.
После вычислений получим

 

ЗАДАНИЕ N 31 сообщить об ошибке
Тема: Пространственный и косой изгиб

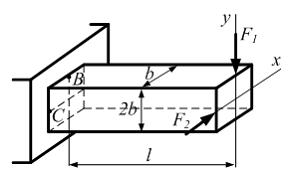
Стержень прямоугольного сечения с размерами b и 2 b, длиной l нагружен внешними силами F₁ и F₂. Значение нормального напряжения в точке В будет равно значению нормального напряжения в точке С, когда отношение равно …

 

Решение:
Стержень работает на косой изгиб. Нормальное напряжение при косом изгибе в точке поперечного сечения с координатами x, y определяется по формуле
В сечении, где требуется определить нормальные напряжения в точках В и С, изгибающие моменты
Осевые моменты инерции сечения относительно главных центральных осей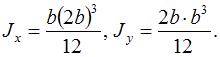
В точке В с координатами , с учетом знака напряжения,
В точке С с координатами , с учетом знака напряжения,

Из условия равенства напряжений в точках В и С получим, что отношение

 

ЗАДАНИЕ N 32 сообщить об ошибке
Тема: Виды нагружения стержня

При заданном варианте нагружения внешними силами стержень прямоугольного сечения с размерами b и 2 b испытывает …

			растяжение, кручение, плоский поперечный изгиб
			растяжение, кручение, плоский чистый изгиб
			растяжение, кручение, чистый косой изгиб
			растяжение, плоский поперечный изгиб

 

ЗАДАНИЕ N 33 сообщить об ошибке
Тема: Расчет простейших статически неопределимых систем

На рисунке показана ферма нагруженная силой F. Жесткость поперечных сечений стержней ЕА, 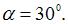Продольные силы в стержнях 1, 2, 3, соответственно, равны: …

			0, F, – F

 

Решение:

Ферма (рис. 1) один раз статически неопределима. Для раскрытия статической неопределимости используем метод сил. На рисунках 2 и 3 показаны основная и эквивалентная система. Каноническое уравнение метода сил имеет вид
На рисунке 4 показано грузовое состояние основной системы. Продольная сила в первом стержне
Рассматривая равновесие узла (рис. 6), определяем продольные силы в стержнях 2 и 3. На рисунке 5 показано единичное состояние основной системы. Продольная сила в первом стержне
Рассматривая равновесие узла (рис. 7), определяем продольные силы в стержнях 2 и 3. 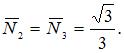Коэффициенты канонического уравнения определим с помощью интеграла Мора.

Подставляя значения в каноническое уравнение, получаем Следовательно продольные силы в стержнях фермы равны:

 

ЗАДАНИЕ N 34 сообщить об ошибке
Тема: Статическая неопределимость. Степень статической неопределенности
В статически определимой системе с помощью уравнений равновесия статики можно определить …

			реакции опор и внутренние силовые факторы
			только реакции опор
			только внутренние силовые факторы
			не все реакции опор и внутренние силовые факторы

 

Решение:
В статически определимой системе с помощью уравнений равновесия статики можно определить реакции опор и внутренние силовые факторы.

 

ЗАДАНИЕ N 35 сообщить об ошибке
Тема: Метод сил
Система канонических уравнений метода сил имеет вид Величина 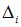это перемещение в направлении i -ой отброшенной связи, вызванное …

			внешней нагрузкой
			реакциями отброшенных связей
			реакциями отброшенных связей и внешней нагрузкой
			силой

 

Решение:
Левую часть канонического уравнения можно трактовать как перемещение в направлении i -ой отброшенной связи вызванное реакциями отброшенных связей и внешней нагрузкой. 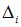– перемещение в направлении i -ой отброшенной связи вызванное внешней нагрузкой.

 

ЗАДАНИЕ N 36 сообщить об ошибке
Тема: Определение перемещений с помощью интегралов Мора. Правило Верещагина

Консольная балка длиной 2 l нагружена внешними силами. Жесткость поперечного сечения на изгиб 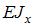по длине постоянна. Прогиб концевого сечения достигнет величины когда значение силы F равно … (Влиянием поперечной силы на величину прогиба пренебречь).

 

Решение:
При определении прогиба концевого сечения используем интеграл Мора, который вычислим по способу Верещагина. Построим, используя метод сечений, эпюру изгибающих моментов от внешней нагрузки (рис. 1 б).
Эпюра М построена на сжатом слое.

К сечению, прогиб которого необходимо определить, прикладываем единичную силу , а внешнюю нагрузку снимаем (рис. 1 в). Построим эпюру изгибающих моментов от единичной силы (рис. 1 г). Далее проводим перемножение эпюр. Находим площадь эпюры изгибающих моментов от внешней нагрузки на каждом участке и умножаем на ординату единичной эпюры, расположенную под центром тяжести эпюры моментов от внешних сил. Складывая результаты перемножения, находим
При перемножении эпюр необходимо учитывать, по какую сторону от оси расположены площадь и ордината.
Из условия, что прогиб концевого сечения равен , получим

 

 

 

Преподаватель: Секретов М.В.
Специальность: 150400.62 - Технологические машины и оборудование
Группа: ГМО-09
Дисциплина: Сопротивление материалов
Идентификатор студента: Клочков Я.А.
Логин: 06ps776353
Начало тестирования: 2012-12-12 15:05:31
Завершение тестирования: 2012-12-12 15:35:18
Продолжительность тестирования: 29 мин.
Заданий в тесте: 36
Кол-во правильно выполненных заданий: 11
Процент правильно выполненных заданий: 30 %

ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Внутренние силы и напряжения

Интегральная связь между крутящим моментом () и касательными напряжениями имеет вид …

 

Решение:

Площадь сечения можно разбить прямоугольной координатной сеткой на элементарные площадки. и – равнодействующие касательных напряжений, действующих на элементарной площадке, − элементарные моменты относительно оси z.
Крутящий момент определяется как сумма элементарных моментов. Заменяя суммирование интегрированием по площади сечения, получаем

 

ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Модели прочностной надежности
Материал полностью заполняет объем тела и имеет беспустотную, бездефектную структуру. Данная гипотеза называется гипотезой …

			сплошной среды
			однородности
			изотропности
			абсолютной упругости

 

ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Основные понятия, определения, допущения и принципы
Древесина – материал …

			анизотропный
			кристаллический
			изотропный
			аморфный