Оценка облигаций
Общая формула для определения текущей рыночной цены облигаций с позиции инвестора (PV) имеет следующий вид:
где: FT – сумма, выплачиваемая при погашении облигации; In – ежегодные процентные выплаты; i – требуемая инвестором норма дохода; n – конкретный период времени (год); Т – число лет до момента погашения облигации. Самый простой случай – оценка облигаций с нулевым купоном. Поскольку денежные поступления по годам (кроме последнего) равны нулю, стоимость облигации будет определяться по следующему уравнению:
Бессрочная облигация предусматривает неопределенно долгую выплату дохода, поэтому при расчете ее стоимость определяется из уравнения
При оценке облигаций с постоянным доходом денежный поток складывается из одинаковых по годам поступлений и нарицательной стоимости облигации, выплачиваемой в момент погашения: причем ежегодные процентные выплаты постоянны из года в год. Оценка облигаций с плавающим купоном может быть проведена по формуле
причем ежегодные процентные выплаты меняются из года в год. Для оценки облигаций могут использоваться купонная доходность, текущая доходность и конечная доходность (доходность к погашению). Купонная доходность (Yk), устанавливаемая при выпуске облигации, рассчитывается по формуле
где: I – годовой купонный доход; N – номинальная цена облигации. Текущая доходность (YT) определяется по формуле
где: PV – цена, по которой облигация была приобретена инвестором. Конечная доходность (доходность к погашению) (YП) определяется следующим образом:
|

 (3)
(3) (4)
(4) (5)
(5)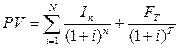 (6)
(6)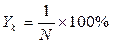 (7)
(7) (8)
(8)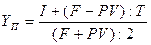 (9)
(9)


