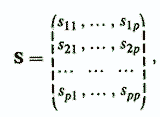Структура экспериментально-психологических данных и свойства линейных диагностических моделей

Без применения эмпирико-статистического анализа не обходится ни одна серьезная попытка конструирования или адаптации тестов /Шмелев А. Г., Похилько В. И., 1985/. Исходным материалом для такого анализа служат результаты экспериментального обследования репрезентативной выборки испытуемых с помощью «чернового» варианта психодиагностического теста. Из полученных данных формируется двумерная таблица экспериментальных данных (ТЭД).

В приведенной таблице приняты следующие обозначения:

N — общее количество объектов (испытуемых);

p — общее количество признаков;

x_j — «j»-й признак (в дальнейшем наряду с термином «признак» будут употребляться также термины «показатель» и «переменная»);

Таблица 2. Таблица экспериментальных данных

Объекты (испытуемые)	Исходные признаки
x1 x2... xj... xp
х1 x2... xi... хN	x11 x12... x1j... x1p x21 x22... x2j... x2p ... xi1 xi2... xij... xip ... xN1 xN2... xNj... xNp

Xij — значение «j»го признака, измеренное у «i»-го объекта.

В соответствии с данной символикой приняты также обозначения:

x =(x₁,...,x _р)' — вектор признаков (знак «()'» означает транспонирование);

х _i =(x _i1,..., x_ip)'—«i»-й объект;

X ={x_i} — множество объектов.

Особенностью психодиагностических экспериментальных данных является то, что исходные признаки x_i, как правило, измерены в номинальных и порядковых (ординальных) шкалах /Суппес П. и др., 1967; Пфанцагль И., 1976; Айвазян С. А. и др., 1983/. Для большинства тестов с закрытыми ответами типа «Выбор», «Восстановление частей» и «Переструктурирование» между возможными вариантами ответов испытуемых нельзя априорно установить ни количественных отношений, ни отношений порядка. Это — номинальные измерения.

В теории измерений номинальные шкалы считаются простейшими и самыми «бедными» (их называют также шкалами наименований и классификационными шкалами). Если обозначить числами возможные варианты ответов испытуемого на тестовые задания, то эти числа будут иметь смысл только абстрактных символов, обозначающих каждый вариант ответов и никакие другие отношения между указанными числами, кроме их равенства, значения не имеют. При сравнении двух испытуемых по признаку, измеренному в номинальной шкале, можно сделать единственный вывод о совпадении или несовпадении значения признака. Поэтому при анализе таких признаков каждую отметку номинальной шкалы считают отдельным самостоятельным признаком. Он принимает всего два значения А и В и разность (А — В) уже может интерпретироваться как степень важности несовпадения данного признака при сравнении двух объектов. Чаще всего применяют значения А=0 и В=1, то есть признак равен либо 0, либо 1, а степень важности признака x_i задается весом w_i, на который умножается x_i. Такие признаки называют двоичными, бинарными, булевыми, а в психодиагностике часто используют термин «дихотомические признаки». Процедура преобразования исходных показателей в набор признаков с двумя градациями носит название дихотомизации /Миркин Б. Г., 1980/. После проведения дихотомизации номинальные измерения становятся доступны для применения широкого спектра различных методов многомерного количественного анализа с учетом специфики данного вида измерений.

К ординальным переменным относятся, например, признаки, даваемые психодиагностическими методиками с закрытыми ответами на тестовые задания типа «Оценивание». Также иногда в качестве исходных признаков для построения нового диагностического показателя используются значения различных психологических шкал и факторов, которые, являясь нормативными измерениями, с очень большой осторожностью следует относить к количественным измерениям. Для ординальных признаков существенен лишь порядок градаций на шкале, и для них считаются допустимыми любые монотонные преобразования, не нарушающие этот порядок. Методологически строгим является применение к ординальным признакам методов обработки, результат которых инвариантен относительно допустимых преобразований порядковой шкалы /Енюков И. С., 1986/. Поэтому количественный анализ ординальных переменных, как и дихотомических, имеет свою специфику. В то же время некоторые авторы (например, Филмер П. и др., 1978) отмечают, что даже тогда, когда измерения осуществляются в шкалах порядка или более высокого уровня, анализ данных разумно строить так, как будто мы имеем дело с номинальными шкалами.

Описанные выше особенности экспериментальных данных в психодиагностике следует учитывать при выборе диагностической модели и методов эмпирико-статистической оценки ее параметров. В этой диагностической модели должна в определенной форме выражаться связь измеряемого вектора признаков х с тестируемым свойством, которое в дальнейшем будет обозначаться как у. То есть должен быть раскрыт механизм преобразования у=у(х). Первое требование, предъявляемое к математической модели, — это необходимое требование к конечному результату, который обязан быть максимально точным и надежным. Второе требование — лаконичность и интерпретируемость способа получения конечного результата. Указанные требования находятся в тесной взаимосвязи. Чем более экономно по форме и содержательно по смыслу преобразование у=у(х) при соблюдении заданной точности модели, тем более общие закономерности структуры экспериментальных данных вскрывает используемая модель и, значит, тем более устойчива и надежна количественная оценка диагностируемого показателя, получаемая с помощью преобразования у(х).

Структура экспериментальных данных, особенности которой в контексте решаемой диагностической задачи описывает математическая модель, отражается посредством двух основных категорий взаимоотношений между элементами ТЭД — категорий сходства и различия. Сходство и различие объектов ТЭД определяется мерами близости (удаления), а признаков — мерами связи. Ординальный и дихотомический характер исходных признаков выражается в специфике этих мер, которые рассматриваются ниже.

Матрица связи задает отношение «признак-признак» и представляет собой двумерную симметричную квадратную матрицу размера рхр

где Sij — мера связи между признаками x_i и x_j.

Известно большое количество мер связи между признаками. Они отличаются как объемом вычислений, так и теми аспектами связи, которые они отражают. Различные авторы предлагают разные основания для классификации этих мер связи (например, Елисеева И. И. и др., 1977; Миркин Б. Г., 1980; Никифоров А. М. и др., 1988). Здесь будут рассмотрены две представительные группы связи между признаками /Статистические методы..., 1979/.

В первой группе используется принцип ковариации, а во второй — принцип сопряженности признаков. Исходя из первого принципа, заключение о наличии связи между переменными делается в том случае, когда увеличение значения одной переменной сопровождается устойчивым увеличением или уменьшением значений другой. В математическом выражении задача сводится к вычислению ковариации, то есть сопутствующего изменения численных значений признаков. Сюда относится в первую очередь коэффициент корреляции Пирсона (r _kj), который представляет собой произведение моментов и является мерой линейной связи двух переменных x_k и x_j. Он вычисляется по формуле

Многие меры связи отличаются от приведенного коэффициента корреляции Пирсона внешней формой, но являются, по сути, алгебраическим преобразованием этого коэффициента, учитывающим специфику (тип) сопоставляемых признаков. Taк, например, коэффициент ранговой корреляции Спирмена (r_s), часто применяемый для анализа ординальных переменных, представляет собой алгебраическое упрощение r_kj. То же самое можно сказать о точечном бисериальном коэффициенте корреляции (r_pb) который служит мерой связи между дихотомической и количественной переменными. Некоторые другие коэффициенты, в частности тетрахорический коэффициент корреляции (r_tet) и бисериальный коэффициент корреляции (r_bis), можно интерпретировать как аппроксимации r_kj для определенных типов признаков /Гласе Дж. и др., 1976/.

Несколько иной подход в рассматриваемой группе мер связи основывается на подсчете числа несовпадений в ранжировке объектов по сопоставляемым переменным. Этот подход разработал М. Кендалл /1974/, когда предпринял попытку истолковать процесс измерения связи между переменными, не прибегая к принципу произведения моментов. Он рассмотрел два порядковых признака x_i и х_j, на каждый из которых N объектов отображаются в N последовательных рангов (1, 2,..., N). Из N объектов формируется N(N — l)/2 пар, и для каждой пары подсчитывается количество совпадений порядка на признаке xj с порядком на признаке xj. Это количество обозначается «Р». Таким же образом определяется количество несовпадений (инверсий) «Q».

Коэффициент ранговой корреляции, получивший название «тау» Кендалла, вычисляется по формуле

Несмотря на различие в подходах, между коэффициентами ранговой корреляции Спирмена и Кендалла, как отмечается в /Гласе Дж. и др., 1976/, существует тесная логическая связь. В то же время τ Кендалла имеет интересную для математических статистиков интерпретацию: если из N объектов случайно выбираются два объекта, то разность между вероятностью того, что они будут иметь одинаковый порядок как по x_i, так и по x_j, и вероятностью того, что у них будет наблюдаться различие в порядках по x_i и х_j, равна величине τ («тау»). На основе подсчета количества совпадений и инверсий сконструирован целый ряд различных мер связи. В частности, этот принцип используется в коэффициенте бисериальной ранговой корреляции Кертена и Гласса (r_rb), который применяется для изучения взаимодействия дихотомической и порядковой переменных. В то же время Гласc/Glass G. V., 1966/ показал, что r_rb аналогичен бисериальному коэффициенту корреляции для порядковых переменных и для его вычисления можно обойтись без подсчета совпадений и инверсий.

Вторая обширная группа мер связи, основанная на принципе взаимной сопряженности, направлена на выяснение следующего факта: появляются ли некоторые значения одного признака одновременно с определенными значениями другого чаще, чем это можно объяснить случайным стечением обстоятельств. В данном случае фиксируется только сам факт наличия или отсутствия интересующих значений признака независимо от их количественного выражения /Никифоров А. М. и др., 1988/. Общим, как бы переходным, для первой и второй групп мер связи является популярный в психодиагностических исследованиях коэффициент φ;, который предназначен для измерения связи двух дихотомических признаков или, иными словами, для анализа таблиц сопряженности 2X2 (табл. 2).

Таблица 2.Таблица сопряженности дихотомических признаков

Признак xj	Признак xi	Итог
	а	b	a+b
	с	d	c+d
Итог	a+c	b+d

Коэффициент φ; представляет собой алгебраическое упрощение обычного коэффициента корреляции Пирсона r_ij с учетом специфики дихотомических признаков и вычисляется по формуле

Другие меры связи, основанные на принципе взаимной сопряженности, например коэффициенты Чупрова, Крамера, контингенции Пирсона и т. д., подробно рассматриваются в /Кендалл М. и др., 1976; Миркин Б. Г., 1976; Елисеева И. И. и др., 1977; Статистические методы..., 1979; Айвазян С. А. и др., 1983/.

Таблица 3. Рекомендуемые меры связи между различными типами признаков

Тип признака	Тип признака
Дихотомический	Ординальный	Количественный
Дихотомический (бинарная шкала)	1. Коэффициент φ(Пирсона) 2. Тетрахорический коэффициент корреляции (rtet)	1. Рангово-бисериальный коэффициент корреляции Кертена и Гласса (rrb)	1. Точечный бисериальный коэффициент корреляции (rpb) 2. Бисериальный коэффициент корреляции (rbis)
Ординальный (шкала порядка)		1. Коэффициент ранговой корреляции Спирмена. 2. Тау Кендалла (τ)	1. Коэффициент ранговой корреляции Спирмена (rs) 2. Тау Кендалла (τ)
Количественный (шкала интервалов или отношений)			Коэффициент корреляции Пирсона (rij)

В целом по проблеме выбора той или иной меры связи для решения конкретной задачи можно сказать следующее. Применение к одним и тем же данным различных мер связи нередко приводит к отличающимся результатам. Это обусловлено тем, что математики, конструировавшие коэффициенты корреляции, как правило, исследовали их свойства в предельных ситуациях — около 0 или 1 /Елисеева И. И. и др., 1977/. Поведение же различных мер связи внутри интервала [0,1] сравнительно мало изучено. Поэтому на практике предпочтительный выбор какой-либо меры связи бывает непросто обосновать, а результаты использования разных мер трудно сравнивать. Во многом такой выбор определяется личными симпатиями исследователя. В качестве рекомендации предлагается таблица 3, в которую сведены наиболее часто употребляемые в психологии меры связи для признаков разного типа. Подробно все коэффициенты, указанные в таблице, анализируются в /Гласc Дж. и др., 1976/.

Матрица близостей (удаленностей) задает отношение «объект-объект» и представляет собой квадратную симметричную матрицу NхN с неотрицательными элементами

Элементы d_ij являются значениями некоторой меры близости (удаленности) между объектами х_i и х_j. Чаще в анализе данных используются меры удаленности. К этим мерам предъявляются следующие требования:

1. Максимальное сходство объекта с самим собой —

2. Требование симметрии —

3. Выполнение неравенства треугольника -

Последнее требование предъявляется к матрицам расстояний (диагональные элементы должны быть равны нулю). Матрица D, удовлетворяющая перечисленным трем требованиям, допускает толкование структуры взаимоотношений объектов исследования как некоторой геометрической конфигурации точек в многомерном пространстве признаков.

Приведем наиболее распространенные меры расстояния между объектами х_i и х_j
.

1) Евклидово расстояние -

Эта мера может применяться для вычисления расстояния между объектами, описанными количественными, качественными и дихотомическими признаками. Ее использование целесообразно, когда признаки однородны по смысловой нагрузке и одинаково важны для решаемой задачи.

2) Взвешенное евклидово расстояние —

Данную меру используют, когда необходимо количественно шразить важность каких-либо признаков или выравнять мас-птабы неоднородных признаков.

3) Расстояние Махаланобиса -

де S — ковариационная матрица генеральной совокупности, из соторой извлечены объекты х_i и х_j
. Ее элементы вычисляются по формуле S_ki(см. выше). Эта мера применяется при сильной зависимости и неоднородности исследуемых признаков, так как она инвариантна к линейным преобразованиям пространства признаков (изменению масштаба и повороту осей).

4) Расстояние Минковского —

Это расстояние еще называют «городской метрикой», поскольку в данном случае расстояние между точками определяется аналогично расстоянию вдоль взаимно перпендикулярных улиц городских кварталов /Александров В. В. и др., 1990/. Городская метрика применяется для измерения расстояния между объектами, описанными ординальными признаками. I _k(х_i, х_j
) равно разнице номеров градаций по k-му признаку у сравниваемых объектов х_i и х_j
.

5) Расстояние Хэмминга -

Данная мера наиболее часто используется для определения различий между объектами, задаваемыми дихотомическими признаками и интерпретируется как число несовпадений значений признаков у рассматриваемых объектов х_i и х_j
. Для дихотомических признаков она соответствует квадрату евклидова расстояния. Так же как и для евклидова расстояния, может применяться взвешенное расстояние Хэмминга.

6) Другие меры близости для дихотомических признаков.

Эти меры близости обычно основаны на подсчете числа нулевых или единичных компонент признаков, совпавших или несовпавших на объектах х_i и х_j
, и придании этому числу различной степени важности. Подробно указанные меры рассматриваются в /Боннер Р. Е., 1969; Житков Г. Н., 1970; Елисеева И. И. и др., 1977/.

Представление информации о структуре экспериментальных данных посредством матриц связей признаков S и близостей (удаленностей) объектов D служит промежуточным звеном в процессе построения диагностических моделей у = у(х) различного типа. Независимо от этого типа различают две основные стратегии определения параметров диагностических моделей. Первая стратегия использует методы, опирающиеся непосредственно только на особенности конфигурации образовавшейся структуры экспериментальных данных, находящей свое выражение в числовых отношениях сходства и различия элементов ТЭД. Поэтому она называется стратегией, основанной на критерии автоинформа тивности экспериментальных данных. Например, если в матрице связей S обнаруживается группа сильно коррелирующих признаков, то, возможно, это является следствием отражения признаками, вошедшими в группу, эмпирического фактора, соответствующего требуемому диагностическому конструкту. Или, например, если, исходя из анализа компонент матрицы расстояний D, удается установить, что распределение объектов в пространстве признаков состоит из нескольких геометрических группировок, то это может быть основанием для попытки объяснить данный факт различиями изучаемых объектов по тестируемому свойству и построить адекватный диагностический алгоритм.

В то же время нужно хорошо представлять, что выявляемые группировки объектов в большой степени зависят от типа используемой меры расстояния между объектами и от используемой системы признаков. Так, в частности, «хорошая» с точки зрения решаемой диагностической задачи геометрическая структура распределения объектов в каком-либо подпространстве признаков может быть «развалена» добавлением к этому подпространству «шумящих» признаков или «подавлена» более «сильной» структурой, отражающей иррелевантный тестируемому свойству фактор. В свою очередь, значимые связи между признаками могут образовываться за счет расслоения выборки объектов под действием постороннего фактора. И, наоборот, отсутствие корреляций может объясняться влиянием неучтенной характеристики выборки (например, для лиц разного пола корреляции каких-либо признаков могут быть высокими, но иметь противоположные знаки. Поэтому в смешанной выборке корреляции этих же признаков будут близки к нулю).

Приведенные примеры, а также другие примеры, рассматриваемые в последующих разделах, показывают, что нередко для построения диагностической модели требуется привлечение дополнительной информации, кроме той, которая непосредственно содержится в исходной ТЭД. Эту дополнительную информацию называют обучающей, и ее несут сведения об эмпирических отношениях между объектами исследования, полученные тем или иным способом. Обучающая информация формируется по так называемым критериям внешней информативности или, иными словами, внешним критериям. Данная информация представляется в различных формах. Это может быть привязка к объектам значений «зависимой» переменной, измеренной в количественной шкале, номер однородного по тестируемому свойству класса, порядковый номер (ранг) объекта х_i
в ряду всех объектов, упорядоченных по степени проявления диагностируемого свойства, и, наконец, совокупности значений набора внешних (не включенных в анализируемую ТЭД) признаков, характеризующих тестируемый психологический феномен. При использовании обучающей информации объекты в исходном пространстве признаков в соответствии с внешним критерием как бы «окрашиваются в разнообразные цвета», что позволяет более целенаправленно находить способы преобразования исходных признаков в результирующий диагностический показатель. Методы, основанные на применении внешних критериев, составляют вторую стратегию определения параметров диагностических моделей.

В зависимости от совпадения критериев автоинформативности с критериями внешней информативности методы первой и второй стратегии могут приводить к сходным результатам. В то же время эти результаты в значительной мере зависят от того, с помощью каких преобразований раскрывается информационный потенциал исходных экспериментальных данных. Не существует диагностической «информативности вообще». Информативность данных существует только по отношению к применяемому типу диагностической модели, выбор которой, в свою очередь, определяется техническими ресурсами и теоретическими представлениями конкретных исследователей.

В психодиагностике превалируют линейные модели, в которых результирующий показатель представляется в виде взвешенной суммы исходных признаков

Распространенность линейных моделей объясняется прежде всего их наибольшей простотой, понятностью и «удоборешаемостью», позволяющей, в частности, вручную обрабатывать результаты тестирования. Например, лаборант, участвующий в психодиагностическом эксперименте, сравнивает ответы испытуемого на вопросы теста со специальным «ключом», суммирует совпадения с определенными весами и тем самым реализует линейную диагностическую модель.

С математической точки зрения развитие диагностики происходит в направлении отказа от линейных моделей /Айвазян С. А. и др., 1989/. Но, несомненно, они всегда будут иметь большое прикладное значение благодаря лаконичности и хорошей интерпретируемости.

Линейные модели удобны для рассмотрения геометрических иллюстраций вычисления результирующего показателя. Уравнение у(х)=0 — это уравнение гиперплоскости в пространстве признаков (рис.), а расстояние от объекта х_i
, который отображается точкой в данном пространстве, до гиперплоскости равно

 

—
норма весового вектора w.

На рис. изображены два объекта х_i и х_j
и кусок плоскости у(х) = 0 в трехмерном пространстве. Так как в данном случае норма весового вектора выбрана произвольно и равна 1, расстояния от х_i и х_j
до плоскости непосредственно соответствуют значениям у(х_i
) и у(х_j
). Указанные значения часто бывает удобно интерпретировать как проекции х_i и х_j
на любую прямую в рассматриваемом пространстве признаков, перпендикулярную плоскости у(х)=0 Эта прямая обозначена на рисунке у(х).

 

Точка ее пересе
чения с плоскостью дает значение нуля на прямой. В дальнейшем будут неоднократно использоваться подобные геометрические иллюстрации. Это будет уместно и тогда, когда норма весового вектора не равна единице, так как искажение масштаба, которое наблюдается в данном случае, не повлечет за собой искажения главного — взаимного расположения проекций точек на прямую.

Рис. Иллюстрация линейной диагностической пространстве признаков модели в трехмерном пространстве признаков.

 

В зависимости от угла зрения, под которым рассматривается линейная диагностическая модель, она может иметь различные названия. Если, например, «у» трактуется как «зависимая» переменная, для которой ищется функциональная связь с «независимыми» переменными (признаками) x_i, то уравнение линейной модели

 

у(х)
называется линейной функцией регрессии или уравнением множественной регрессии. Если рассматривается задача классификации объектов, то у=у(х) обычно называют линейной решающей функцией, а уравнение у(х)=0 — разделяющей границей или уравнением разделяющей гиперплоскости. Ниже при обсуждении того или иного метода определения параметров линейной диагностической модели тоже будут использоваться различные термины, но, как указывалось выше, глобальным атрибутом для разграничения этих методов является привлечение или не привлечение критерия внешней информативности.