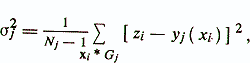Типологический подход

Публикации, посвященные типологическому подходу, обычно рассматривают его в рамках психопрогностики (например, Ямпольский Л. Т., 1986; Кулагин Б. В. и др., 1989). Известна точка зрения, которая разделяет психопрогностику и психодиагностику /Забродин Ю. М., 1984/. В то же время с позиции формального математического аппарата психопрогностика и психодиагностика имеют много общего. И в том и в другом случае испытуемый описывается набором чисел (р-мерным вектором признаков), точно так же каждому испытуемому ставится в соответствие значение некоторого критериального показателя z, и задача состоит в том, чтобы построить математическую модель, имеющую максимальную корреляцию с z или дискриминирующую испытуемых подобно z. Конечно, чем продолжительнее временной интервал, на который распространяется прогноз, тем с более серьезными трудностями сталкивается исследователь при определении критериального показателя и тем сложнее может оказаться структура модели у=у( х). Но, так или иначе, в данном изложении не будет проводиться граница между понятиями психопрогностики и психодиагностики, а внимание будет сконцентрировано большей частью на феноменологии процедуры обработки экспериментальных данных, получившей название типологического подхода.

Целесообразность применения типологического подхода обусловлена недостаточной эффективностью линейных диагностических моделей. Так, Л. Т. Ямпольский /1986/ отмечает, что это простейший способ интеграции индивидуальных факторов в реальное поведение и что психологические факторы (исходные признаки в диагностической модели. — В. Д.) могут взаимодействовать более сложным образом. В /Кулагин Б. В. и др., 1989/ рассматриваются проблемы построения диагностических моделей в целях профотбора и указывается, что, как правило, совокупность обследуемых кандидатов идеализированно считается однородной выборкой из некоторой генеральной совокупности и модель прогнозирования успешности профессиональной деятельности оказывается усредненной для всех испытуемых, включенных в обследование. Это приводит к снижению доли совпадения прогноза с реальной профессиональной успешностью, которая в данном случае практически никогда не превышает 70-80%. Далее рассуждения приведенных выше авторов хотя и несколько различаются, но приводят к одинаковым выводам. Эти рассуждения примерно таковы.

В условиях неоднородности обучающей выборки линейные диагностические модели должны смениться нелинейными. Однако решение задачи построения нелинейных моделей затруднено из-за отсутствия априорных сведений о виде искомых функций у=у(х). В таких случаях эффективный результат может быть достигнут с помощью методов кусочно-линейной аппроксимации у=у( х). В свою очередь, успешность кусочно-линейной аппроксимации зависит от того, насколько хорошо удается разбить испытуемых на однородные группы, для каждой из которых в отдельности строится собственная линейная диагностическая модель. Это можно рассматривать как индивидуализацию диагностического правила, которая заключается в выборе одной из нескольких функций у=у (х) для каждого испытуемого с учетом его принадлежности той или иной группе.

Таким образом, процедура построения диагностической модели состоит из двух этапов. На первом этапе производится разбиение всего множества испытуемых X={х_i}, i=1,N на М однородных групп G_j( X= UG_j ), j= 1,M На втором этапе для каждой группы G_j вырабатывается линейное диагностическое правило y_j=y_j( х) с помощью рассмотренных выше методов линейного регрессионного или дискриминантного анализа. Соответственно процедура собственно диагностики также осуществляется в два приема. Сначала определяется принадлежность испытуемого х_i к одной из ранее выделенных групп G_j и затем для диагностики х_i применяется требуемая диагностическая модель y_j = y_j( х).

«Слабое звено» данного подхода заключается в трудно формализуемом и нечетком определении понятия однородности группы объектов. Как известно, задаче разбиения объектов на однородные группы уделяется значительное место в общей проблематике анализа данных. Методы решения этой задачи носят разные названия: автоматическая классификация, распознавание без учителя, таксономия, кластерный анализ, расщепление смеси и т. д., но имеют одинаковую сущность. Все они в явной или неявной форме опираются на категорию близости (различия) объектов в пространстве признаков. Для решения задачи выделения однородных групп объектов исследования необходимо дать ответы на три основных вопроса:

а) какие признаки будут считаться существенными для описания объектов?

б) какая мера будет применяться для измерения близости объектов в пространстве признаков?

в) какой будет выбран критерий качества разбиения объектов на однородные группы?

На каждый из приведенных вопросов существует много вариантов ответов, и в зависимости от выбранного ответа можно получить совершенно различные разбиения объектов на однородные группы. Поэтому решение конкретной задачи выделения однородных групп объектов всегда не лишено субъективной оценки исследователя. В следующей главе будут более подробно рассмотрены возможные алгоритмы разбиения множества объектов на группы в рамках общей проблемы анализа многомерной структуры экспериментальных данных. Здесь же ограничимся рекомендациями, изложенными в /Ямпольский Л. Т., 1986; Кулагин Б. В. и др., 1989/, полезность которых подтверждена значимыми практическими результатами.

В работе /Кулагин Б. В. и др., 1989/ рекомендуется для группирования испытуемых отбирать признаки, хорошо дискриминирующие массив исходных данных и слабо коррелирующие между собой. Кроме того, набор этих признаков должен быть минимизирован. Л. Т. Ямпольский /1986/ предлагает выделять группировки объектов в пространстве общих факторов, полученных методами факторного анализа исходного пространства признаков. И в той и в другой работе важное, если не решающее, значение придается психологическому осмыслению выделяемых группировок испытуемых. Возможность четкой интерпретации полученных группировок как определенных психологических типов служит достаточно веским доводом в пользу не случайного разбиения испытуемых на группы, которое могло бы произойти под действием какого-либо иррелевантного решаемой диагностической задаче фактора (отсюда, собственно, и проистекает название «типологический подход»).

Оценка качества диагностической модели, полученной в результате применения типологического подхода, обычно осуществляется путем сравнения с обычной линейной диагностической моделью, построенной без разделения объектов обучающей выборки на группы. Например, используется следующий показатель

где σ²₀ — остаточная дисперсия обычной линейной регрессионной модели, а σ²_T вычисляется по формуле

Здесь σ²_j — остаточная дисперсия регрессионной диагностической модели у _j = у _j ( х) для группировки G_j, определяемая из выражения

где N — общее количество испытуемых;
N_j — число испытуемых в группировке G_j;
М — число группировок.

Также для проверки гипотезы об идентичности обычной линейной регрессионной модели и набора регрессионных уравнений у_j=y_j(х) может быть использован F-критерий Фишера /Елисеева И. И. и др., 1977/

Эффективность типологического подхода по сугубо формальным соображениям не может быть ниже эффективности обычной линейной диагностической модели, которую можно рассматривать как вырожденный случай кусочно-линейной модели. В то же время кроме практического выигрыша типологический подход имеет определенную теоретическую ценность — он раскрывает взаимосвязь диагностики психологических черт, как группировок признаков, и психологических типов, как группировок испытуемых. Идеалом типологического подхода, замечает Б. В. Кулагин /1984/, является разработка такого метода, который позволит для каждой отдельной индивидуальности выбирать оптимальную диагностическую модель.