Метод контрастных групп

Исходной информацией при использовании метода контрастных групп, помимо таблицы экспериментальных данных с результатами обследования испытуемых «черновым» вариантом психодиагностического теста, является также «черновая» версия линейного правила вычисления тестируемого показателя. Эта «черновая» версия может быть составлена экспериментатором, исходя из его теоретических представлений о том, какие признаки и с какими весами должны быть включены в линейную диагностическую модель. Кроме того, «черновая» версия может быть почерпнута из литературных источников, когда у экспериментатора возникает потребность адаптировать опубликованный психодиагностический тест к новым условиям. Метод контрастных групп применяется также в составе процедуры повышения внутренней согласованности заданий ранее отработанного теста.

В основе метода контрастных групп лежит гипотеза о том, что значительная часть «черновой» версии диагностической модели подобрана или угадана правильно. То есть в правую часть уравнения у_ч = у_ч(х) вошло достаточно много признаков, согласованно отражающих тестируемое свойство. В то же время в «черновой» версии у_ч(х) определенная доля признаков приходится на ненужный или даже вредный балласт, от которого нужно избавиться. Как и во всех других методах, опирающихся на категорию внутренней согласованности, это означает, что в пространстве признаков, включенных в исходную диагностическую модель, распределение объектов вписывается в эллипсоид рассеивания, вытянутый вдоль направления диагностируемой тенденции. В свою очередь, влияние информационного балласта выражается в уменьшении такой вытянутости эллипсоида рассеивания, так как «шумящие» признаки увеличивают разброс исследуемых объектов по всем другим направлениям. При этом «зашумление» основной тенденции будет тем сильнее, чем ближе к центру распределения располагаются диагностируемые объекты, и тем слабее, чем ближе к полюсам главной оси эллипсоида рассеивания находятся рассматриваемые объекты. Это связано с тем, что попадание объектов в крайние области объясняется, главным образом, кумулятивным эффектом согласованного взаимодействия информативных признаков. Описанные представления о структуре экспериментальных данных лежат в основе следующей процедуры, которая будет рассмотрена на примере анализа пунктов при конструировании тест-опросников /Шмелев А. Г., Похилько В. И., 1985/.

Сначала назначаются исходные шкальные ключи (веса) w˚_j для пунктов теста (дихотомических признаков) х_j. Для каждого i-го испытуемого подсчитывается суммарный тестовый балл

Обычно абсолютные значения весов w_j определяют приблизительно и часто берут равными единице. Поэтому направление

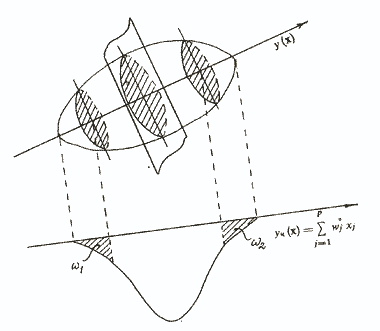
будет несколько отличаться от направления главной диагонали эллипсоида рассеивания у(х) (рис. 3).

Рис. 3. Иллюстрация метода контрастных групп

Но если ориентировочно у_ч(х) правильно отражает диагностируемое свойство, то на краях распределения суммарного балла, построенного по всем объектам исследуемой выборки, можно выделить контрастные группы ω₁ и ω₂, в которые войдут объекты с минимальными погрешностями, вносимыми «шумящими» признаками. Эти группы не должны быть слишком малы. Для нормального распределения, как правило, берут контрастные группы объемом 27% от общего объема выборки, для более плоского — 33%. В принципе считается приемлемой любая цифра от 25 до 33% /Анастази А., 1982/. Следующий шаг заключается в определении степени связи каждого пункта с дихотомической переменной — номером контрастной группы. Мерой этой связи может служить так называемый коэффициент различения, представляющий собой разницу процентов того или иного ответа на анализируемый пункт в полярных группах испытуемых. Наиболее часто используется коэффициент связи Пирсона φ, который затем сравнивается с граничным значением

где χ²_гр — стандартный квантиль распределения χ² с одной степенью свободы. Обычно ориентируются на 5% и 1% уровни \ значимости, для которых значение χ² равно 3,84 и 6,63 соответственно. Если для і-гo пункта |φ_і|<|φ_гр|, то весовому коэффициенту w_i присваивается значение нуля, то есть признак х_i исключается из линейной диагностической модели у_ч(х). Таким образом проверяются все пункты «чернового» варианта теста. Затем для оставшихся пунктов вся процедура снова полностью повторяется и т. д.

На практике не встречается случая, когда окончательно отобранные с помощью приведенной процедуры информативные признаки абсолютно бы совпали с первоначально заданными. Сходимость этой процедуры зависит от исходного соотношения «хороших» и «плохих» заданий теста. По-видимому, для диагностических моделей, основанных на принципе внутренней согласованности используемых признаков, в каждой конкретной задаче существует определенный порог соотношения информативных и «шумящих» признаков, начиная с которого возможно возникновение эффекта самоорганизации или самосовершенствования диагностической модели посредством описанного выше алгоритма.