Линейные операции над векторами. 1. Охарактеризуйте систему органів панівної верхівки Великого князівства Литовського.
1. Охарактеризуйте систему органів панівної верхівки Великого князівства Литовського. 2. Назвіть органи місцевого управління Великого князівства Литовського. 3. Охарактеризуйте систему органів панівної верхівки Речі Посполитої. 4. Назвіть органи місцевого управління Речі Посполитої. 5. Назвіть військові органи. Література: 1. Рішення Люблінського сейму про об’єднання Польщі і Литви в одну державу – Річ Посполиту (1569). 2. Захарченко П.П. Історія держави і права України.: Університет «Україна», 2005. 3. Іванов В.М. Історія держави і права України в 2-х ч. – К.: 2002. 4. Іванов В.М. Історія держави і права України: Навчальний посібник. – К.: Атіка, 2007. 5. Історія держави і права України: Посіб. Для підготов. до іспитів / В.І. Орленко. В.В. Орленко. – 3-е вид., доповн. та перероб. – К.: Вид. Паливода А.В., 2008. 6. Історія держави і права України / За ред.. В.Я. Тація, А.Й. Рогожина. – К.: Ін Юре, 2000. 7. Кульчицький В.С., Тищик Б.Й. Історія держави і права України: Навч. посіб. – К.:Атіка, 2001. 8. Музиченко П. Історія держави і права України: навч. посіб. – К.: «Знання», КОО,2006. 9. Хрестоматія з історії держави і права України. У 2-х т. / За ред.. В.Г. Гончаренка. – К.: Ін Юре, 1997.
Векторная алгебра
Основные понятия
Величины, встречающиеся в механике, физике и других прикладных науках, могут быть разделены на два типа: скалярные и векторные. Величины, которые определяются только одним числовым значением, называются скалярными или скалярами (например, масса, время, температура, цена и т. д.). Величины, для определения которых требуется задать кроме числа еще и направление, называются векторными (например, скорость, ускорение, сила и т. д.). Геометрически их изображают вектором. Определение 1. Вектором называется направленный отрезок, то есть отрезок прямой с указанием точек начала Обозначать вектор в этом случае будем так:
Длину вектора (или модуль вектора) обозначают так: Определение 2. Если длина вектора равна единице, то он называется единичным или ортом. Обозначается – Определение 3. Если у вектора начало и конец совпадают, то его длина равна нулю и его называют нулевым, например, Определение 4. Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными (параллельными) – рисунок 2.
На рисунке 2 векторы В математике обычно рассматривают свободные векторы, то есть когда положение их начала не играет никакой роли. Определение 5. Векторы
То есть вектор Определение 6. Векторы, лежащие в одной плоскости (или в параллельных плоскостях), называются компланарными. Очевидно, что любые два вектора компланарны, а три вектора не всегда можно «уложить» в одну плоскость.
Линейные операции над векторами
К линейным операциям над векторами относятся: сложение векторов и умножение вектора на число. Определение 1. Сумой
Иногда два вектора удобнее складывать по правилу параллелограмма. Для этого векторы переносят так, чтобы начала их были в одной точке
Пусть требуется сложить
Определение 2. Разностью Если два вектора Два вектора равной длины, лежащие на одной прямой и направленные в противоположные стороны, называются взаимнообратными: если один из них обозначается символом Определение 3. Произведением
Любой вектор
Теорема 1. Два ненулевых вектора Справедливы легко проверяемые свойства: 1) 2) 3) 4) 5) Эти свойства позволяют выполнять действия с векторными выражениями так же, как и с алгебраическими. Например,
|

 и конца
и конца  .
. (первая буква
(первая буква  – начало, вторая –
– начало, вторая –  – конец вектора) или одной буквой
– конец вектора) или одной буквой 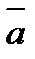 , которую пишут в конце вектора (рисунок 1).
, которую пишут в конце вектора (рисунок 1).
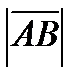 ,
,  .
.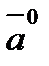 .
.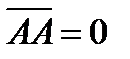 . Направление нулевого вектора не определено.
. Направление нулевого вектора не определено.
 ,
, 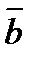 и
и 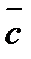 коллинеарны, при этом векторы
коллинеарны, при этом векторы  и
и  одинаково направлены (
одинаково направлены (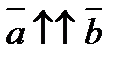 ), а векторы
), а векторы 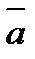 и
и 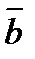 и
и  ,
,  ).
).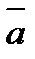 и
и  называются равными, если они имеют одинаковую длину, параллельны и одинаково направлены. Кратко
называются равными, если они имеют одинаковую длину, параллельны и одинаково направлены. Кратко ,
,  , если он может быть получен при помощи параллельного переноса.
, если он может быть получен при помощи параллельного переноса. двух векторов
двух векторов 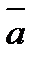 и
и 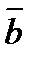 называется новый вектор, который идет из начала вектора
называется новый вектор, который идет из начала вектора 
 . Затем строят параллелограмм со сторонами, равными
. Затем строят параллелограмм со сторонами, равными  и
и  . Вектор
. Вектор  будет вектор, совпадающий с диагональю этого параллелограмма, идущий из общего начала
будет вектор, совпадающий с диагональю этого параллелограмма, идущий из общего начала  и
и 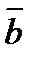 (точки
(точки 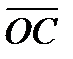 (рисунок 4).
(рисунок 4).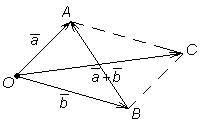
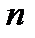 векторов
векторов 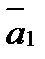 ,
,  ,
, 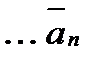 . Суммой этих векторов будет вектор
. Суммой этих векторов будет вектор 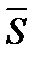 , соединяющий начало
, соединяющий начало  при условии, что начало каждого совмещено с концом предыдущего (рисунок 5).
при условии, что начало каждого совмещено с концом предыдущего (рисунок 5).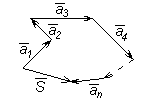
 двух векторов
двух векторов 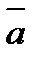 и
и  называется вектор, который в сумме с вектором
называется вектор, который в сумме с вектором  составляет вектор
составляет вектор 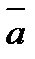 .
.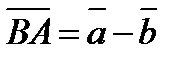 .
. . Тогда
. Тогда 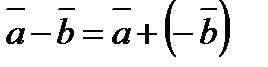 . Таким образом, построение разности равносильно прибавлению к «уменьшаемому» вектору, обратного «вычитаемому».
. Таким образом, построение разности равносильно прибавлению к «уменьшаемому» вектору, обратного «вычитаемому». вектора
вектора 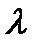 (или также
(или также  ) называется вектор, модуль которого равен произведению модуля вектора
) называется вектор, модуль которого равен произведению модуля вектора 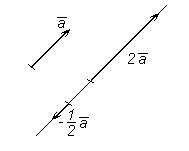
 и единичного вектора
и единичного вектора  того же направления, что и вектор
того же направления, что и вектор  или
или 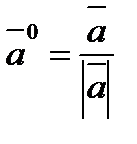 .
.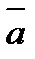 и
и 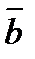 параллельны тогда и только тогда, когда существует такое единственное число
параллельны тогда и только тогда, когда существует такое единственное число 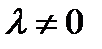 , что
, что 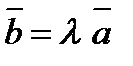 . Это необходимое и достаточное условие коллинеарности двух векторов.
. Это необходимое и достаточное условие коллинеарности двух векторов.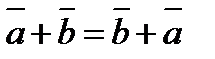 ,
,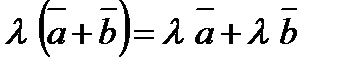 ,
, ,
,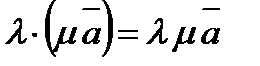 ,
,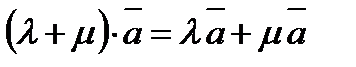 .
.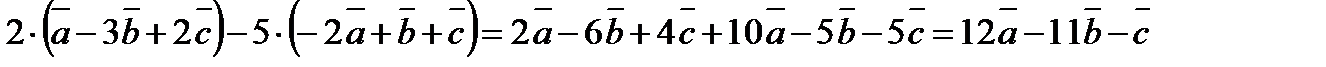 .
.


