Координаты вектора. Линейные операции над векторами в координатной форме
Определение 1. Координаты вектора – это его проекции на соответствующие оси. Отрезки
Проекции:
То есть координаты вектора равны разности между координатами конца и начала. Из
тогда
то есть длина вектора равна корню квадратному из суммы квадратов его координат. Аналогично и в 3-хмерном пространстве:
где
Определение 2. Минимальное количество векторов, через которые можно выразить любой вектор назовем базисом. Так на прямой базисом является один вектор
На плоскости базисом являются два неколлинеарных вектора Определение 3. Тройка векторов 1) вектор 2) каждый из векторов 3) векторы
Из рисунка 7:
где
и
тогда
Итак, вектор задается или координатами Аналогично и в 3-хмерном пространстве. Каким бы ни был вектор
коэффициенты этого разложения являются проекциями вектора Теорема. Линейным операциям над векторами соответствуют в точности такие же операции над их координатами. Например,
тогда
Если векторы параллельны, то их координаты пропорциональны
Пример 1. Задача №776 Клетеник Д.В. Проверить коллинеарность векторов Решение. 1. Проверим коллинеарность:
Следовательно, векторы коллинеарны, так как их координаты пропорциональны. Коэффициент пропорциональности
2. Действительно
Пример 2. Задача №775 Клетеник Д.В. Даны два вектора 1) 2) 3) 4) 5) Решение. Решим первую и пятую задачи: 1) Ответ: проекция на ось 5) Ответ:
|

 ,
,  обозначим
обозначим  и
и  ,
,  обозначим
обозначим  . Тогда вектор
. Тогда вектор  (рисунок 7) имеет координаты
(рисунок 7) имеет координаты .
.
 ,
,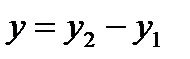 .
.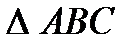 по теореме Пифагора, если
по теореме Пифагора, если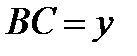 ,
, 
 ,
, ,
, имеет координаты
имеет координаты 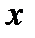 ,
,  ,
,  , которые в дальнейшем будем обозначать в скобках
, которые в дальнейшем будем обозначать в скобках .
. (рисунок 8). Через него выразим вектор
(рисунок 8). Через него выразим вектор 
 .
.
 и
и  (рисунок 7).
(рисунок 7). ,
, 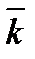 называется координатным базисом, если эти векторы удовлетворяют следующим условиям:
называется координатным базисом, если эти векторы удовлетворяют следующим условиям: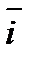 лежит на оси
лежит на оси  , вектор
, вектор 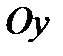 , вектор
, вектор  ;
;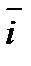 ,
,  ,
, 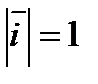 ,
,  ,
,  .
.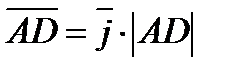 ,
, ,
,
 .
. ,
,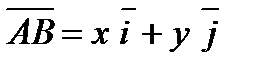 . (1)
. (1) , или выражением (1), которое называется разложением вектора по координатному базису.
, или выражением (1), которое называется разложением вектора по координатному базису. , он всегда может быть разложен по базису
, он всегда может быть разложен по базису  ;
; ,
,  ,
,  суть проекции вектора
суть проекции вектора 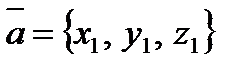 ,
,  ,
, ,
, .
. .
.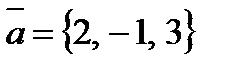 и
и  . Установить какой из них длиннее другого и во сколько раз, как они направлены – в одну сторону или в противоположные стороны.
. Установить какой из них длиннее другого и во сколько раз, как они направлены – в одну сторону или в противоположные стороны. .
.
 в 3 раза и векторы направлены в противоположные стороны.
в 3 раза и векторы направлены в противоположные стороны. ,
,  .
.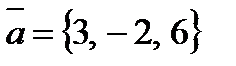 и
и  . Определить проекции на координатные оси следующих векторов:
. Определить проекции на координатные оси следующих векторов: ;
; ;
; ;
; ;
; .
.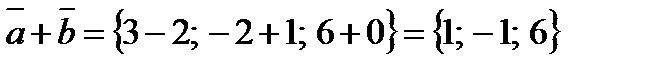 .
. ; на ось
; на ось  ; на ось
; на ось  .
. ,
, 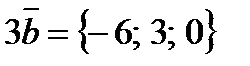 ,
,  .
. ;
; 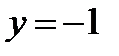 ;
;  .
.


