| 
| 
|
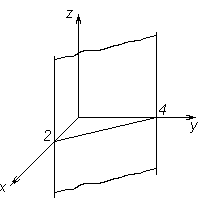
Рисунок 22 – Плоскость 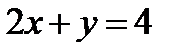
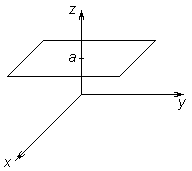
| Рисунок 23 – Плоскость 
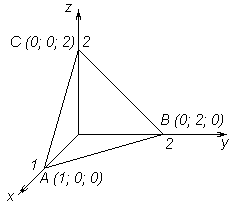
| Рисунок 24 – Плоскость 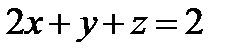
|
Уравнение 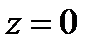 – плоскость
– плоскость 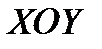 .
.
Уравнение  – плоскость
– плоскость  .
.
Уравнение 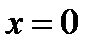 – плоскость
– плоскость  .
.
Задача 1. Через точку  проведем плоскость
проведем плоскость 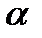 , перпендикулярную вектору
, перпендикулярную вектору 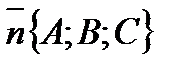 (рисунок 25).
(рисунок 25).
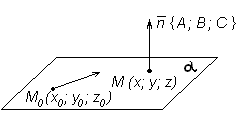
|
| Рисунок 25
|
Для решения этой задачи на плоскости 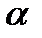 возьмем текущую точку
возьмем текущую точку  . Векторы
. Векторы 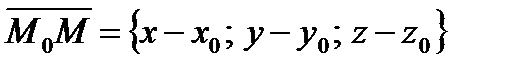 и
и 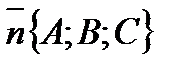 перпендикулярны, значит их скалярное произведение равно нулю, то есть
перпендикулярны, значит их скалярное произведение равно нулю, то есть
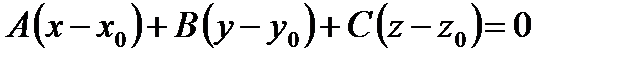 . (19)
. (19)
Это уравнение плоскости, проходящей через точку  и перпендикулярной вектору
и перпендикулярной вектору 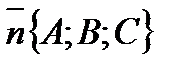 .
.
Вектор 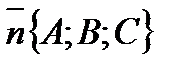 , перпендикулярный плоскости
, перпендикулярный плоскости 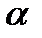 , называется нормалью плоскости.
, называется нормалью плоскости.
Преобразуем уравнение (19):
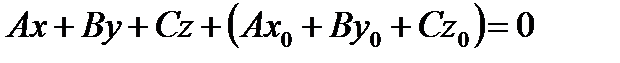
и переобозначим через
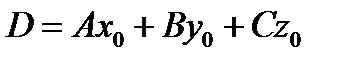 .
.
Получим уравнение (18).
Задача 2. Через три точки провести плоскость.
Пусть даны точки 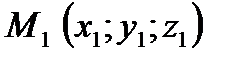 ;
; 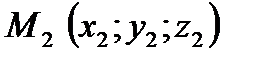 ;
; 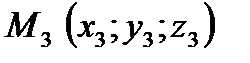 и для вывода уравнения возьмем четвертую точку – текущую
и для вывода уравнения возьмем четвертую точку – текущую  (рисунок 26).
(рисунок 26).
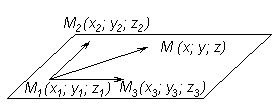
|
| Рисунок 26
|
Проведем векторы  ,
,  и
и 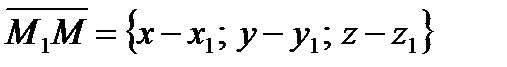 . И так как эти векторы компланарны, то их смешанное произведение равно нулю, то есть
. И так как эти векторы компланарны, то их смешанное произведение равно нулю, то есть
 . (20)
. (20)
Задача 3. Пусть плоскость отсекает на осях 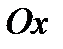 ;
; 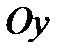 ;
;  соответственно отрезки
соответственно отрезки 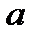 ;
;  ;
;  , то есть плоскость проходит через три точки
, то есть плоскость проходит через три точки 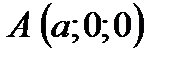 ;
; 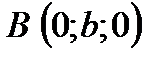 ;
; 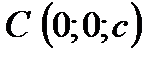 (рисунок 27).
(рисунок 27).
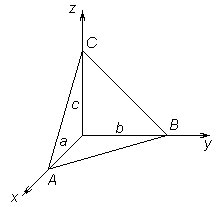
|
| Рисунок 27
|
Подставив координаты этих точек в уравнение (20), получим:
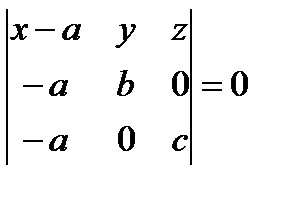 .
.
Раскроем определитель и получим
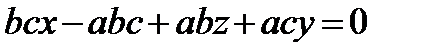 или
или 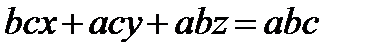 .
.
Поделим обе части на  , получим
, получим
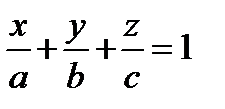 (21)
(21)
– уравнение плоскости в отрезках.
Если умножить обе части общего уравнения (18) на нормирующий множитель  , взяв его со знаком, противоположным знаку свободного члена, то получим уравнение плоскости
, взяв его со знаком, противоположным знаку свободного члена, то получим уравнение плоскости
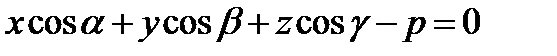 , (22)
, (22)
которое называется нормальным. Где углы 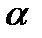 ;
; 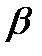 ; и
; и 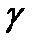 – это углы между векторами нормали плоскости с соответствующими осями
– это углы между векторами нормали плоскости с соответствующими осями  ;
; 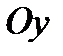 ;
;  .
.
Расстояние от точки  до плоскости находят по формулам:
до плоскости находят по формулам:
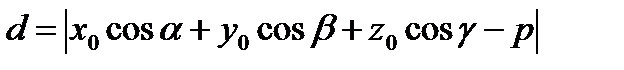 (23)
(23)
или
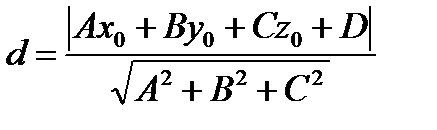 , (24)
, (24)
подставив координаты точки в нормальное уравнение плоскости.
Под углом между плоскостями 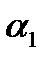 и
и 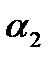 понимается один из двугранных углов, образованных этими плоскостями.
понимается один из двугранных углов, образованных этими плоскостями.
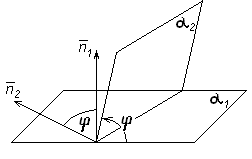
Двугранный угол измеряется линейным, например, это угол  , который равен углу между нормалями, как углы с соответственно перпендикулярными сторонами (рисунок 28).
, который равен углу между нормалями, как углы с соответственно перпендикулярными сторонами (рисунок 28).
|
| Рисунок 28
|
Так что, если заданы две плоскости:
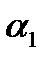 :
:  ,
,  .
.
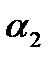 :
: 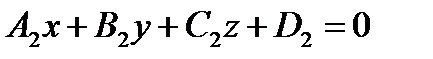 ,
, 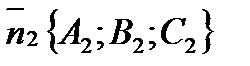 , то
, то
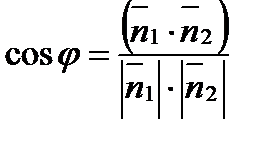 .
.
В координатной форме:
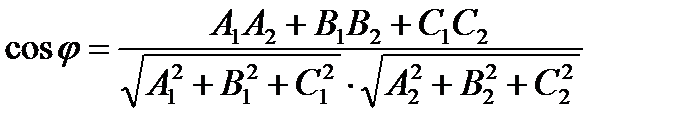 . (25)
. (25)
Если плоскости перпендикулярны, то и их нормали  , но тогда
, но тогда 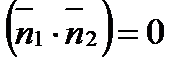 . Тогда
. Тогда
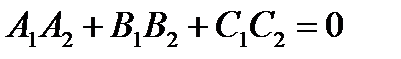 (26)
(26)
– условие перпендикулярности двух плоскостей.
А если плоскости параллельны, то и их нормальные векторы  , значит, координаты этих векторов будут пропорциональны, то есть
, значит, координаты этих векторов будут пропорциональны, то есть
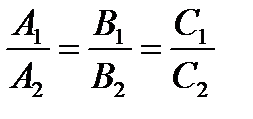 (27)
(27)
– это условие параллельности двух плоскостей.




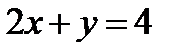

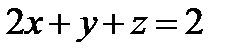
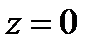 – плоскость
– плоскость 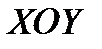 .
. – плоскость
– плоскость  .
.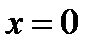 – плоскость
– плоскость  .
. проведем плоскость
проведем плоскость 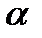 , перпендикулярную вектору
, перпендикулярную вектору 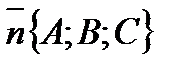 (рисунок 25).
(рисунок 25).
 . Векторы
. Векторы 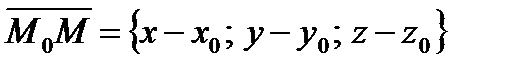 и
и 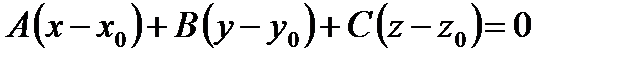 . (19)
. (19)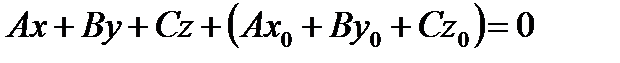
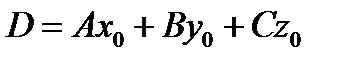 .
.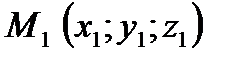 ;
; 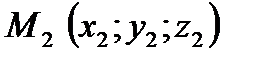 ;
; 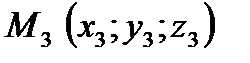 и для вывода уравнения возьмем четвертую точку – текущую
и для вывода уравнения возьмем четвертую точку – текущую 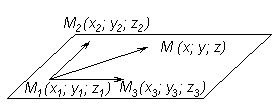
 ,
,  и
и 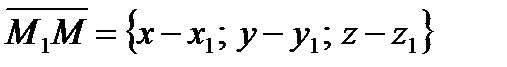 . И так как эти векторы компланарны, то их смешанное произведение равно нулю, то есть
. И так как эти векторы компланарны, то их смешанное произведение равно нулю, то есть . (20)
. (20)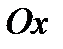 ;
; 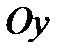 ;
;  соответственно отрезки
соответственно отрезки 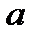 ;
;  ;
;  , то есть плоскость проходит через три точки
, то есть плоскость проходит через три точки 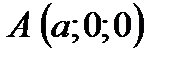 ;
; 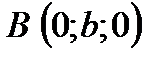 ;
; 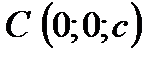 (рисунок 27).
(рисунок 27).
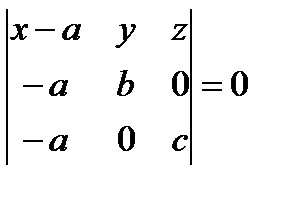 .
.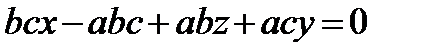 или
или 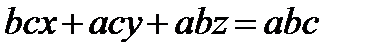 .
. , получим
, получим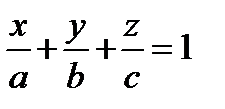 (21)
(21) , взяв его со знаком, противоположным знаку свободного члена, то получим уравнение плоскости
, взяв его со знаком, противоположным знаку свободного члена, то получим уравнение плоскости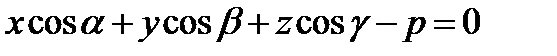 , (22)
, (22)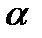 ;
; 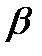 ; и
; и 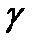 – это углы между векторами нормали плоскости с соответствующими осями
– это углы между векторами нормали плоскости с соответствующими осями  ;
; 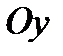 ;
;  .
.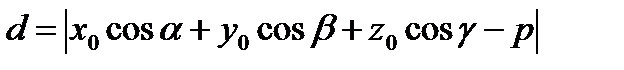 (23)
(23)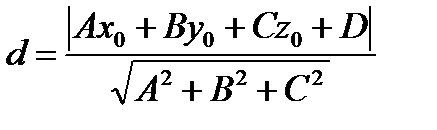 , (24)
, (24)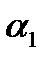 и
и 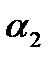 понимается один из двугранных углов, образованных этими плоскостями.
понимается один из двугранных углов, образованных этими плоскостями. , который равен углу между нормалями, как углы с соответственно перпендикулярными сторонами (рисунок 28).
, который равен углу между нормалями, как углы с соответственно перпендикулярными сторонами (рисунок 28).
 ,
,  .
.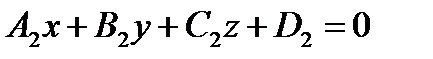 ,
, 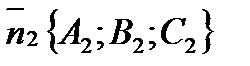 , то
, то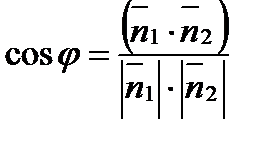 .
.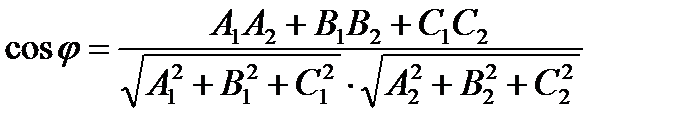 . (25)
. (25) , но тогда
, но тогда 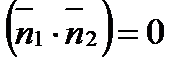 . Тогда
. Тогда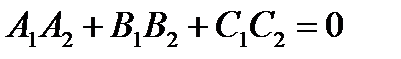 (26)
(26) , значит, координаты этих векторов будут пропорциональны, то есть
, значит, координаты этих векторов будут пропорциональны, то есть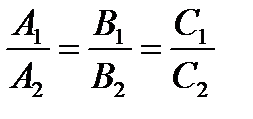 (27)
(27)


