Кривые второго порядка
Эллипс
Определение 1. Эллипсом называется линия, представляющая множество точек плоскости, сумма расстояний которых до двух фиксированных точек, называемых фокусами, есть величина постоянная. Пусть фокусами эллипса являются точки Обозначим сумму расстояний от любой точки эллипса до фокусов через
Для вывода уравнения эллипса введем декартову систему координат так, чтобы ось
При таком выборе системы фокусы имеют координаты Так как одна сторона
Найдем расстояние между двумя точками и подставим в (1):
– это уравнение эллипса. Преобразуем его. Перенесем второй корень в правую часть равенства и возведем обе части равенства в квадрат:
Преобразуем это равенство. Получим:
Еще раз возведем в квадрат:
Перенесем переменные слагаемые в левую часть равенства, а постоянные – в правую:
Так как
Теперь уравнение эллипса примет вид:
Разделим обе части равенства на Окончательно получим каноническое (простейшее) уравнение эллипса:
|
и 
.
(
), а расстояние 
между фокусами через 
(
). Тогда для любой текущей точки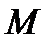 
эллипса будет
, (1)
. (2)
прошла через точки 
поместим в середину отрезка 
(рисунок 35)
; 
.
меньше суммы двух других сторон, то
.
; 
,
.
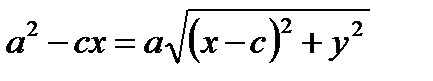. (3)
.
.
, то положим
. (4)
.
.
. (5)
