Угол между двумя прямыми и условия параллельности и перпендикулярности двух прямых
Пусть прямые
В
как внешний угол, угол
тогда
если только
но
поэтому
Если
– это условие перпендикулярности двух прямых.
Полярное уравнение прямой
Полярное уравнение прямой можно определить, указав расстояние
Для любой точки
но
Значит
есть уравнение прямой в полярных координатах.
Нормальное уравнение прямой
Перепишем уравнение (14) в виде:
Учитывая, что в полярной системе координат
получим уравнение
которое называется нормальным уравнением прямой.
Тогда уравнение (16) можно переписать в виде
Чтобы уравнение (4) привести к виду (17) надо обе части его умножить на нормирующий множитель Чтобы найти расстояние от любой точки
|

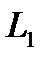 и
и 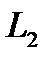 имеют угловые коэффициенты
имеют угловые коэффициенты  и
и 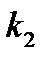 (рисунок 19).
(рисунок 19).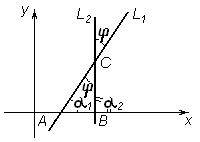
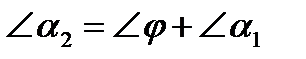
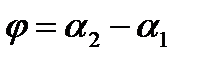 ,
,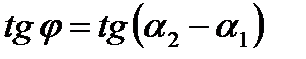 ,
,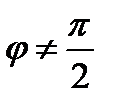 . Тогда
. Тогда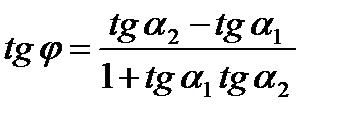 ,
,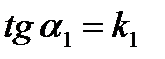 ;
; 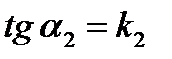 ,
,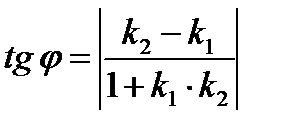 (11)
(11)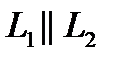 , то
, то 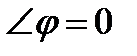 и
и 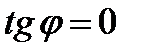 , а это когда числитель дроби (11) равен нулю, то есть, если прямые параллельны, то
, а это когда числитель дроби (11) равен нулю, то есть, если прямые параллельны, то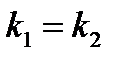 .
.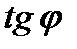 не существует при
не существует при  . А это возможно, когда знаменатель дроби (11) равен нулю, то есть
. А это возможно, когда знаменатель дроби (11) равен нулю, то есть (13)
(13)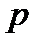 от полюса
от полюса  до данной прямой и угол
до данной прямой и угол  между полярной осью
между полярной осью 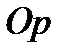 и осью
и осью  , проходящей через полюс
, проходящей через полюс 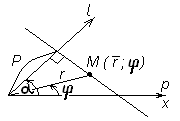
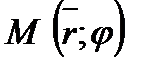 на данной прямой имеем:
на данной прямой имеем: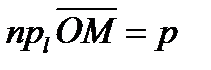 ,
, .
. (14)
(14)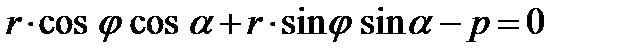 .
.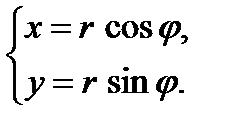 ,
,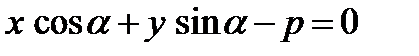 , (16)
, (16) (рисунок 21).
(рисунок 21).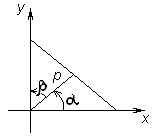
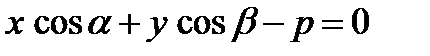 . (17)
. (17) , знак которого выбирают противоположным знаку свободного члена в уравнении (4).
, знак которого выбирают противоположным знаку свободного члена в уравнении (4).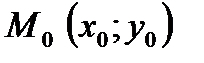 до прямой надо в нормальное уравнение прямой подставить координаты этой точки, то есть
до прямой надо в нормальное уравнение прямой подставить координаты этой точки, то есть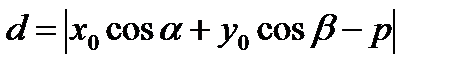 или
или 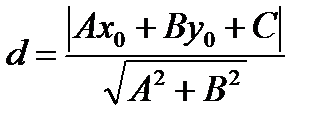 .
.


