Прямая в пространстве
Прямая в пространстве задается как линия пересечения двух плоскостей:
Уравнения (28) называются общими уравнениями прямой в пространстве. Задача 1. Через точку
Решение. Для вывода уравнения возьмем на прямой текущую точку Вектор
Уравнения (29) называются каноническими уравнениями прямой в пространстве. А вектор Обозначим отношения из равенств (29) через
и выразим все переменные
получим уравнения прямой, которые называются параметрическими. Задача 2. Составить уравнение прямой, проходящей через две точки Решение. В качестве направляющего вектора
которые называются уравнениями прямой, проходящей через две данные точки. От общих уравнений прямой (28) можно перейти к каноническим уравнениям (29). Координаты точки Так как прямая перпендикулярна векторам
Замечание. Очевидно, что для одной и той же прямой можно записать много общих уравнений вида (28). А множество плоскостей, проходящих через одну прямую будет:
Это уравнение называется уравнением пучка плоскостей. В нем Чтобы от канонических уравнений прямой перейти к общим, достаточно составить из равенств (29) две различные произвольные пары, например
Угол между прямыми, заданными уравнениями
принимают как угол между направляющими векторами (рисунок 30).
Если прямые
и условие параллельности двух прямых:
Две прямые
Они либо пересекаются, если
|

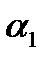 и
и 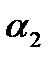
 . (28)
. (28) , параллельно вектору
, параллельно вектору  провести прямую (рисунок 29).
провести прямую (рисунок 29).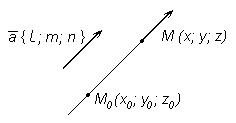
 .
. параллелен вектору
параллелен вектору 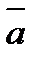 . Значит, их координаты пропорциональны, то есть
. Значит, их координаты пропорциональны, то есть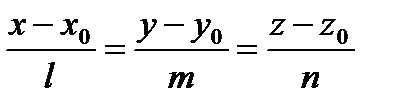 . (29)
. (29)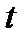

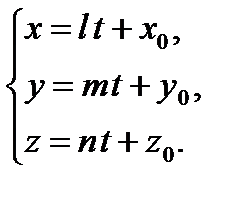 (30)
(30)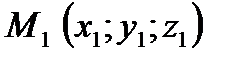 и
и 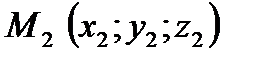 .
. и точку, через которую проходит прямая, возьмем
и точку, через которую проходит прямая, возьмем 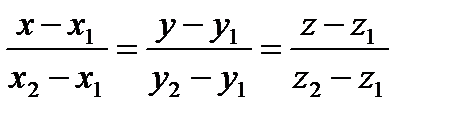 , (31)
, (31)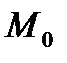 на прямой получаем из системы (28), придав одной из координат произвольное значение (например
на прямой получаем из системы (28), придав одной из координат произвольное значение (например  ).
).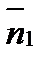 и
и  , то за направляющий вектор прямой можно принять векторное произведение
, то за направляющий вектор прямой можно принять векторное произведение  .
. . (32)
. (32)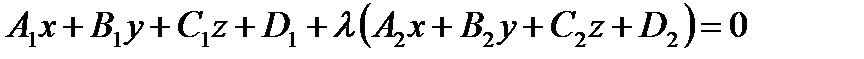 . (33)
. (33) – произвольная постоянная.
– произвольная постоянная.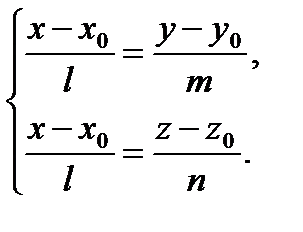 .
.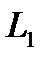 :
: 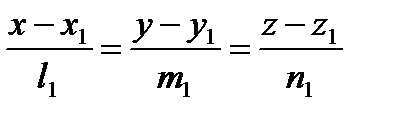 , где
, где 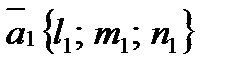 .
.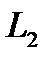 :
: 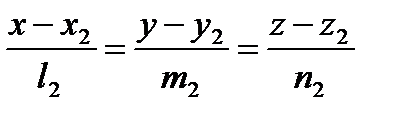 , где
, где 

 ,
,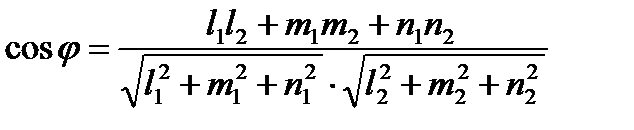 . (34)
. (34)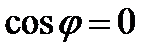 , то есть
, то есть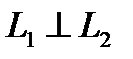 :
:  .
. :
:  .
.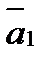 ,
,  и
и  .
.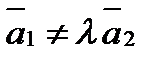 , либо параллельны, если
, либо параллельны, если 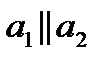 .
.


