Совместные задачи на прямую и плоскость
1) Если в задаче необходимо найти уравнение плоскости, проходящей через прямую, заданную общими уравнениями (28), то лучше воспользоваться уравнением пучка плоскостей (33), и из дополнительных условий найти неизвестный параметр Пример 3. Составить уравнение плоскости, проходящей через прямую а) точку б) параллельную оси Решение. Воспользуемся уравнением пучка плоскостей
отсюда Найденное
Замечание. Если прямая, через которую проходит плоскость, задана каноническими уравнениями, то необходимо перейти от них к общим уравнениям. 2) Если плоскость проходит через точку Пример 4. Составить уравнение плоскости Решение. Так как прямая
Тогда уравнение плоскости по формуле (19) будет:
то есть
3) Угол между прямой и плоскостью – есть угол, образованный прямой и ее проекцией на плоскость. Пусть плоскость Обозначим угол между прямой и плоскостью через
Тогда
Найдем
и тогда, так как
или
Если прямая
Поэтому
– это условие параллельности прямой и плоскости. Если прямая
Поэтому равенства
являются условиями перпендикулярности прямой и плоскости. 4) Чтобы найти точку пересечения прямой и плоскости, надо прорешать систему
Для этого надо: 1) Перейти от канонических уравнений прямой к параметрическим
2) Подставляя эти выражения для 3) Найденное В общем виде это выглядит так:
или
тогда, если прямая
то
Если
и если при этом а) б) если и То есть
является условием принадлежности прямой плоскости.
|

 .
. :
:  и
и ,
, .
. . Так как точка
. Так как точка  принадлежит плоскости, то ее координаты удовлетворяют этому уравнению тождественно. Поэтому
принадлежит плоскости, то ее координаты удовлетворяют этому уравнению тождественно. Поэтому ,
, .
.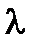 подставим в уравнение пучка плоскостей, и тогда после приведения подобных, уравнение плоскости будет:
подставим в уравнение пучка плоскостей, и тогда после приведения подобных, уравнение плоскости будет: ,
,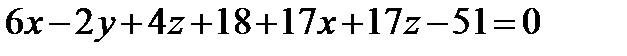 ,
, .
. и известен нормальный вектор
и известен нормальный вектор 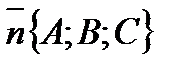 или его легко найти, то лучше воспользоваться уравнением (19).
или его легко найти, то лучше воспользоваться уравнением (19).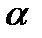 , проходящей через точку
, проходящей через точку  и перпендикулярно прямой
и перпендикулярно прямой  .
. можно принять за нормальный вектор для плоскости (рисунок 31).
можно принять за нормальный вектор для плоскости (рисунок 31).
 ,
, .
. , где
, где 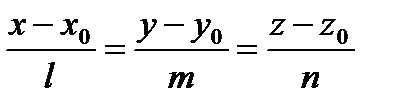 .
. – угол между вектором нормали
– угол между вектором нормали  и направляющим вектором прямой
и направляющим вектором прямой  (рисунок 32).
(рисунок 32).
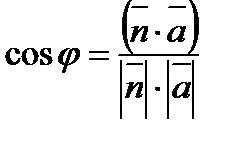 .
. (считая
(считая  )
) , получим
, получим
 . (35)
. (35) (рисунок 33).
(рисунок 33).
 , то есть
, то есть (36)
(36) и
и  параллельны (рисунок 34).
параллельны (рисунок 34).
 (37)
(37)



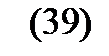
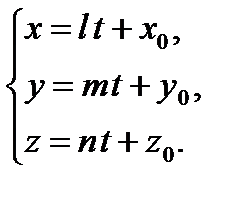 . (40)
. (40) ;
;  и
и  в уравнение (39) и решая его относительно
в уравнение (39) и решая его относительно  , находим
, находим 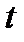 .
.

 ,
, .
. ,
, , то прямая
, то прямая  , то прямая целиком лежит в плоскости
, то прямая целиком лежит в плоскости  (41)
(41)


