Второй способ приведения уравнений эллипса и гиперболы к каноническому виду через собственные числа и собственные векторы квадратичной формы
Рассмотрим на примере. Пример 5 (676).
Решение. 1. Выделим квадратичную форму в уравнении:
2. Составляем матрицу этой квадратичной формы:
– кривая гиперболического типа. 3. Находим собственные числа и собственные векторы этой матрицы. Для этого составляем характеристичекое уравнение:
4. Находим координаты собственных векторов. При
При
5. Нормируем векторы
6. Находим координаты единичных векторов:
7. Составляем ортонормированную матрицу (координаты единичных векторов записаны в столбец):
8. Переходим к новым координатам. Из первой строки матрицы
Из второй строки матрицы
9. Новые координаты подставим в исходное уравнение. После тождественных преобразований получаем в квадратичной форме коэффициент при «
После приведения подобных, имеем:
Данная линия представляет собой гиперболу с центром в точке
|
.
.
,
.
,
,
.
.
.
и 
. Для этого находим их длину:
.
и 
.
.
имеем:
.
.
» равен меньшему собственному числу (
), а коэффициент при «
» равен большему собственному числу (
). Слагаемое с «
» исчезает. Об этом надо помнить и пользоваться, так что новые координаты в исходное уравнение подставлять только в оставшуюся от квадратичной формы часть, то есть:
.
,
,
,
.
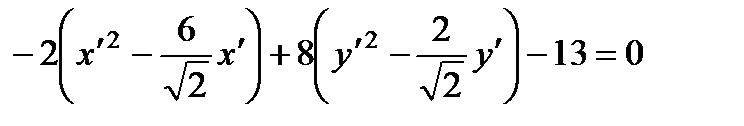и действительной осью 
.
