Прямая на плоскости
Утверждение. Любое уравнение первой степени на плоскости – есть прямая. Уравнение
есть общее уравнение прямой. При
Переобозначив
получим
– это прямая, параллельная оси
Переобозначим
тогда
– это прямая, параллельная оси
эЧтобы убедиться лежит ли точка Пример 1. Принадлежат ли точки Решение. Точка
а точка
Чтобы узнать координаты точки пересечения двух прямых, нужно совместно прорешать систему уравнений, определяющих эти прямые
Если
то есть коэффициенты в уравнениях прямых не пропорциональны, то прямые пресекаются в одной точке. Если коэффициенты при неизвестных в уравнениях прямых и свободные члены пропорциональны, то прямые сливаются (система имеет бесчисленное множество решений). Если коэффициенты пропорциональны, а свободные члены нет, то прямые параллельны (система решений не имеет). Из уравнения (4) выразим «
Переобозначим через
тогда уравнение (5) примет вид:
– уравнение прямой с угловым коэффициентом
Пусть прямая
Вычтем из равенства (7) равенство (8), получим
Это уравнение прямой, проходящей через точку Пусть прямая проходит через две точки Возьмем текущую точку
Векторы
Это уравнение прямой, проходящей через две точки.
|

 (4)
(4) уравнение
уравнение .
.

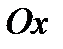 , если
, если  , то
, то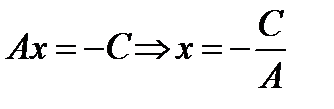 .
. ,
,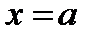
 .
. – уравнение оси
– уравнение оси  – уравнение оси
– уравнение оси  на прямой, необходимо подставить координаты точки
на прямой, необходимо подставить координаты точки  в уравнение этой прямой.
в уравнение этой прямой. и
и  прямой
прямой 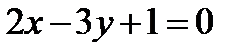 .
. принадлежит прямой, так как
принадлежит прямой, так как ,
, не принадлежит прямой, так как
не принадлежит прямой, так как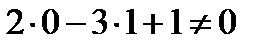 .
. .
. ,
, »
» . (5)
. (5)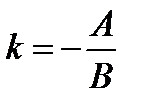 ,
,  ,
, (8)
(8) , где
, где  – угол между прямой и положительным направлением оси
– угол между прямой и положительным направлением оси  » – отрезок
» – отрезок  , где точка
, где точка  , точка
, точка  (рисунок 17).
(рисунок 17).
 проходит через точку
проходит через точку 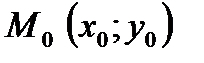 , тогда координаты этой точки удовлетворяют уравнению прямой (7) тождественно, то есть
, тогда координаты этой точки удовлетворяют уравнению прямой (7) тождественно, то есть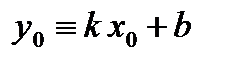 . (8)
. (8)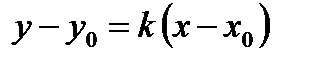 . (9)
. (9) .
. .
. , лежащую на этой же прямой (рисунок 18).
, лежащую на этой же прямой (рисунок 18).
 и
и 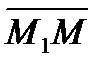 лежат на одной прямой. Координаты их пропорциональны, то есть
лежат на одной прямой. Координаты их пропорциональны, то есть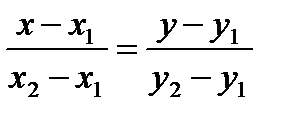 . (10)
. (10)


