Преобразования геодезических и пространственных прямоугольных координат
Вычисление пространственных прямоугольных координат
где
квазигеоида;
Для эллипсоида Красовского полагают
Вычисление геодезических координат а) вычисляют вспомогательную величину б) выполняют анализ величины если
если при этом если если если если в) анализируют значение если иначе выполняют следующее: - вычисляют вспомогательные величины
- присваивают величине
если модуль
В противном случае величине Точность вычислений геодезической широты Контроль поэтапного перехода от одной системы координат к другой выполняют, используя следующие зависимости:
где выраженные в угловых единицах, и геодезическая высота, выраженная в м.;
от одной системы координат Поправки к геодезическим координатам определяют по следующим формулам:
где и высоте,
координат системы координат
координат системы координат
систем координат
эллипсоидов
эксцентриситетов;
полуосей;
первых эксцентриситетов;
сечений;
Эти формулы имеют точность соответственно не ниже 1м, 0.03» и Координаты ИСЗ GPS и ГЛОНАСС отнесены в первую очередь к гринвичской пространственной прямоугольной геоцентрической системе координат, начало которой расположено в центре масс Земли, ось Z направлена к «условному земному полюсу» (CTP – Conventional Terrestrial Pole), который соответствует положению среднего полюса на 1900-1905 гг., исправленному за нутацию. Ось X образована пересечением плоскостей экватора и гринвичского меридиана, а ось Y в плоскости экватора дополняет систему до правой. Геоцентрические системы GPS и ГЛОНАСС установлены независимо: GPS отнесена к системе WGS-84 (World Geodetic System, 1984); ГЛОНАСС – к системе ПЗ-90 (Параметры Земли, 1990). Каждая из этих систем базируется на пунктах самостоятельной космической геодезической сети (КГС) и использует свой референц-эллипсоид. Приведем характеристики этих референц-эллипсоидов:
Напомним, что референц-эллипсоиды ряда государств могут быть ориентированы также путем установления исходных геодезических дат, как, например, эллипсоид Красовского в СК-42. Некоторые фирмы-производители публикуют параметры переходов от геоцентрического эллипсоида WGS-84 к большинству используемых в настоящее время других негеоцентрических систем. Приведем примеры параметров таких переходов, отметив, что во всех них углы разворота осей геоцентрических систем по малости последних приняты равными нулю (т.е. непараллельность малых осей референц-эллипсоидов для всех систем считается отсутствующей):
|

 по геодезическим
по геодезическим  выполняют по формулам:
выполняют по формулам: ;
; ;
; ;
; ;
;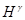 ,
,  - соответственно нормальная высота и высота
- соответственно нормальная высота и высота - радиус кривизны первого вертикала;
- радиус кривизны первого вертикала; - квадрат первого эксцентриситета эллипсоида.
- квадрат первого эксцентриситета эллипсоида. м и
м и  ; для общего земного эллипсоида
; для общего земного эллипсоида  м и
м и  .
. ;
; :
: , то
, то  ;
;  ;
; ;
; , то
, то  ;
; ,
,  , то
, то  ;
; , то
, то  ;
; ,
, 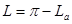 ;
;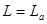 .
. :
: , то
, то  ,
,  ;
; по формулам:
по формулам: ;
; ;
; ;
;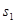 значение нуль и реализуют итеративный процесс вычисления геодезической широты
значение нуль и реализуют итеративный процесс вычисления геодезической широты  :
:
 ;
; ;
; меньше заданного
меньше заданного  , то
, то ;
; ;
; и вычисления повторяют, начиная с вычисления величины
и вычисления повторяют, начиная с вычисления величины  .
. зависит от значения
зависит от значения  погрешность вычисления широты
погрешность вычисления широты 
 - соответственно геодезические широта и долгота,
- соответственно геодезические широта и долгота, - поправки к геодезическим координатам за переход
- поправки к геодезическим координатам за переход к другой
к другой  .
.
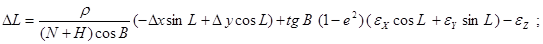


 - геодезические широта, долгота,
- геодезические широта, долгота,  , и высота,
, и высота,  - линейные элементы трансформирования системы
- линейные элементы трансформирования системы - угловые элементы трансформирования системы
- угловые элементы трансформирования системы - дифференциальное различие масштабов
- дифференциальное различие масштабов - разность больших полуосей
- разность больших полуосей - разность квадратов соответствующих
- разность квадратов соответствующих - среднее значение соответствующих больших
- среднее значение соответствующих больших - среднее значение квадратов соответствующих
- среднее значение квадратов соответствующих ;
;  - радиусы кривизны главных нормальных
- радиусы кривизны главных нормальных - сфероидическая функция;
- сфероидическая функция; - число угловых секунд в 1радиане.
- число угловых секунд в 1радиане. , если величины
, если величины  не превышают 0.5 км,
не превышают 0.5 км,  менее 2 ×10-5 , а
менее 2 ×10-5 , а  менее 5». Указанные допуски соответствуют обычно встречающимся значениям элементов ориентирования параметров перехода.
менее 5». Указанные допуски соответствуют обычно встречающимся значениям элементов ориентирования параметров перехода. , м
, м

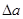 ,
м
,
м

 ,
м
,
м
 ,
м
,
м
 ,
м
,
м



