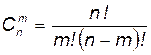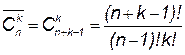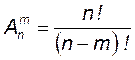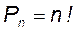Элементы комбинаторики
Комбинаторика – это раздел математики, посвященный решению задач выбора и расположения элементов некоторого конечного множества в соответствии с заданными свойствами. В решении комбинаторных задач применяются основные перечислительные правила: правило умножения и правило сложения. Правило умножения. Пусть требуется выполнить одно за другим (последовательно) k действий. Если первое действие можно выполнить n1 способами, второе n2 способами, и так далее до k -го действия, которое можно выполнить nk способами, то все k действий можно выполнить n1 ∙ n2 ∙… ∙ nk способами. Правило сложения. Если элемент А может быть выбран m способами, а элемент В – n способами, то выбрать либо А, либо В можно m + n способами. Пример 1. В группе 28 человек. Необходимо выбрать старосту и профорга. Сколькими способами это можно сделать? Решение. Старостой может быть выбран любой из 28 студентов, т. е. существует 28 способов выбора старосты. Профоргом можно выбрать любого из оставшихся 27 студентов, так как один уже выбран старостой. Тогда общее число способов выбора старосты и профорга равно Пример 2. Имеется 16 изделий 1-го сорта и 25 изделий 2-го сорта. Необходимо выбрать два изделия одного сорта. Сколько способов выбора двух изделий возможно в данной ситуации?
Решение. По правилу умножения два изделия 1-го сорта можно выбрать
Существуют две схемы выбора m элементов из заданного множества: без возвращения и с возвращением. Схемы выбора без возвращения предполагают, что выбранные элементы не возвращаются в исходное множество. Размещениями из n элементов по m (0 ≤ m ≤ n) называются соединения по m элементов, которые отличаются друг от друга либо хотя бы одним элементом, либо порядком их расположения. Число размещений обозначается символом
Замечание: символ
Пример 3. Студенту необходимо сдать четыре экзамена на протяжении восьми дней. Сколькими способами это можно сделать, если деканатом запрещено сдавать более одного экзамена в день? Решение. Искомое число способов равно
В частном случае, когда выбираются все элементы, т. е. m = n, размещения называются перестановками. Перестановками из n элементов называются соединения, содержащие все n элементов и отличающиеся друг от друга порядком следования элементов. Число перестановок обозначается символом
Пример 4. Сколькими способами можно составить четырехцветный флаг из горизонтальных полос, имея четыре различных цвета? Решение. В данном случае различные флаги отличаются друг от друга лишь порядком цветов. Число возможных флагов равно
Сочетаниями из n элементов по m называются соединения по m элементов, отличающиеся друг от друга хотя бы одним элементом. Число сочетаний из n элементов по m обозначается
Для чисел
Пример 5. Акционерное собрание компании выбирает из 50 человек президента компании, председателя совета директоров и 10 членов совета директоров. Сколькими способами это можно сделать? Решение. Президента компании можно выбрать 50 способами из 50 человек, тогда председателя компании 49 способами, а остальных членов совета директоров
Схемы выбора с возвращением означают, что выбранные элементы возвращаются в исходное множество. Размещения с повторениями. Если в размещении каждый отобранный элемент перед отбором следующего возвращается обратно, то в этом случае рассматриваются размещения с повторениями. Число размещений с повторениями обозначается
где черта указывает на возможность повторения элементов. Пример 6. В конкурсе по 5 номинациям участвуют 10 кинофильмов. Сколько существует способов распределения призов, если по каждой номинации установлены различные премии? Решение. Каждый из вариантов распределения призов представляет собой комбинацию 5 фильмов из 10, отличающуюся от других комбинаций как составом, так и порядком. Поскольку каждый фильм может получить призы как по одной, так и по нескольким номинациям, одни и те же фильмы могут повторяться. Число таких комбинаций равно
Сочетания с повторениями. Если в сочетаниях из n по k некоторые из элементов или все могут оказаться одинаковыми, то такие сочетания называются сочетаниями с повторениями из n по k.Число сочетаний с повторениями обозначается
Пример 7. Сколько наборов из 7 пирожных можно составить, если в продаже имеются 4 сорта? Решение. Искомое число равно
Перестановки с повторениями. Если множество из n различных элементов разбивается на k групп так, что в первую группу попадают k1 элементов,во вторую – k2 элементов, в k-ю группу – km элементов, то число таких разбиений равно
где Пример 8. Наташа получила в подарок 10 просверленных шариков из оргстекла: пять белых, два красных и три голубых. Она продела в них нитку и надела ее как ожерелье на шею. Потом стала менять порядок расположения шариков, и каждый день ожерелье принимало другой вид. Сколько разных видов ожерелья может получить Наташа? Решение. Имеем перестановки с повторениями:
Замечание. Изменение расположения элементов, не меняющее порядка их следования (первый элемент «следует» за последним), называют циклической перестановкой. Если в примере 8 учесть, что ожерелье замкнуто, т. е. последний шарик примыкает к первому, тогда расположение первого элемента не имеет значения. В этом случае окажется, что возможны только 252 различных вида. Пример 9. Сколько существует семизначных чисел, состоящих из цифр 4, 5 и 6, в которых цифра 4 повторяется три раза, а цифры 5 и 6 – по два раза? Решение. Каждое семизначное число отличается от другого порядком следования цифр, при этом фактически все семь мест в этом числе делятся на три группы: на одни места ставится цифра 4, на другие – цифра 5, на третьи места – цифра 6. Таким образом, в нашем случае множество состоит из семи элементов и число таких чисел равно
Запишем основные формулы комбинаторики в табл. 1.1.
Таблица 1.1 Формулы комбинаторики
|

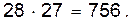
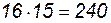 способами. Аналогично, два изделия 2-го сорта можно выбрать
способами. Аналогично, два изделия 2-го сорта можно выбрать 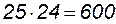 способами. Поэтому общее число способов выбора изделий или 1-го, или 2-го сорта равно
способами. Поэтому общее число способов выбора изделий или 1-го, или 2-го сорта равно 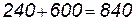 .
.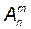 и вычисляется по формуле:
и вычисляется по формуле:
 (читается «эн факториал») обозначает произведение всех натуральных чисел от 1 до n включительно:
(читается «эн факториал») обозначает произведение всех натуральных чисел от 1 до n включительно: .
.
 и вычисляется по формуле:
и вычисляется по формуле: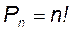
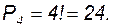
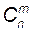 и определяется по формуле:
и определяется по формуле: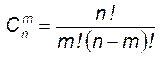 .
.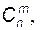 называемых также биномиальными коэффициентами, справедливы следующие тождества:
называемых также биномиальными коэффициентами, справедливы следующие тождества: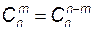 (свойство симметрии);
(свойство симметрии); (рекуррентное соотношение);
(рекуррентное соотношение);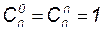 ;
;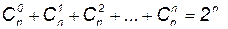 (следствие бинома Ньютона).
(следствие бинома Ньютона).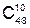 способами. Всего таких соединений можно составить
способами. Всего таких соединений можно составить (по правилу умножения).
(по правилу умножения). и вычисляется по формуле:
и вычисляется по формуле: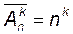 ,
,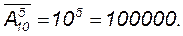
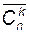 и вычисляется по формуле:
и вычисляется по формуле:
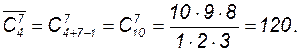
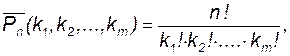
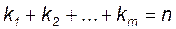 .
.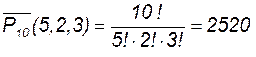 (видов).
(видов).