Случайные величины
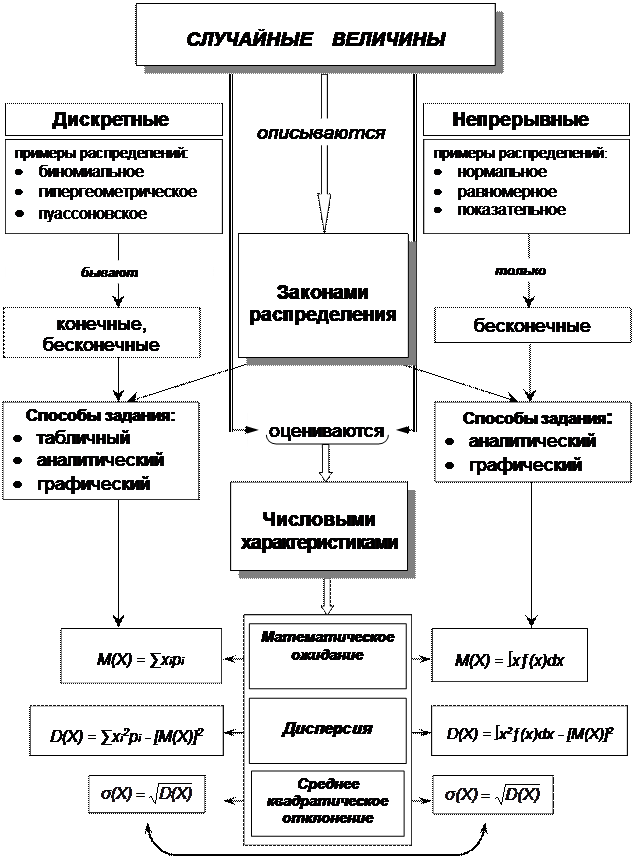
Случайная величина является одним из основных понятий теории вероятностей. Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин. Представим основные сведения по теме «Случайные величины» в виде структурно-логической схемы (рис. 1. 5). При решении многих практических задач важно знать числовые характеристики случайной величины, т. е. числовые параметры, характеризующие наиболее важные черты ее закона распределения. Основными среди них являются характеристики положения (математическое ожидание, медиана и др.) и характеристики рассеяния (дисперсия, среднее квадратическое отклонение и др.).
Рис. 1.5. Случайные величины
Пример 11. Предприниматель рассматривает возможность покупки акций трех предприятий, по каждой из которых известна доходность как отношение величины получаемого дохода за период времени к цене акции и вероятности возможных значений доходности.
Акции какого предприятия следует считать более доходными, если руководствоваться средним значением доходности? Акции какого предприятия являются менее рискованными (считается, что чем выше колеблемость доходности акций, тем больше их рискованность)? Решение. Найдем математическое ожидание (среднее значение) доходности акций каждого предприятия:
Вычислим дисперсию (колеблемость доходности акций):
Таким образом, если руководствоваться средним значением, более доходными следует считать акции третьего предприятия. При этом менее рискованными являются акции первого предприятия.
|