Цепи Маркова и системы массового обслуживания
11.1.–11.24. Задана матрица интенсивностей переходов непрерывной цепи Маркова. Составить размеченный граф состояний, соответствующий матрице, составить систему дифференциальных уравнений Колмогорова для вероятностей состояний; найти предельное распределение вероятностей.
11.1. 
| 11.2. 
| 11.3. 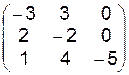
| 11.4. 
| 11.5. 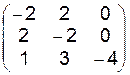
| 11.6. 
| 11.7. 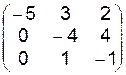
| 11.8. 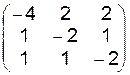
| 11.9. 
| 11.10. 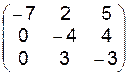
| 11.11. 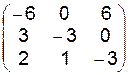
| 11.12. 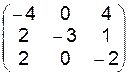
| 11.13. 
| 11.14. 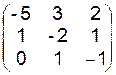
| 11.15. 
| 11.16. 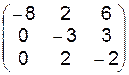
| 11.17. 
| 11.18. 
| 11.19. 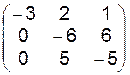
| 11.20. 
| 11.21. 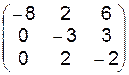
| 11.22. 
| 11.23. 
| 11.24. 
|
12.1.–12.24. Прибор состоит из m узлов, которые могут заменять друг друга. Для работы прибора достаточно, чтобы работал хотя бы один узел. При выходе из строя одного из узлов прибор продолжает нормально функционировать, пока не выйдут из строя все узлы. Поток отказов каждого узла – простейший, среднее время безотказной работы одного узла t часов. При выходе из строя каждый узел начинает сразу ремонтироваться. Время ремонта распределено по показательному закону и в среднем составляет S часов. В начальный момент все узлы исправны.
Найти среднюю производительность прибора, если с выходом из строя каждого узла прибор теряет 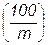 % своей номинальной производительности. % своей номинальной производительности.
| 12. 1. m =3, t =22, S =8.
12.3. m =5, t =10, S =5.
12.5. m =4, t =15, S =3.
12.7. m =3, t =18, S =3.
12.9. m =5, t =15, S =5.
12.11. m =3, t =20, S =4.
12.13. m =3, t =20, S =6.
12.15. m =3, t =16, S =6.
12.17. m =2, t =8, S =2.
12.19. m =4, t =30, S =8.
12.21. m =3, t =20, S =3.
12.23. m =3, t =25, S =7.
| 12.2. m =4, t =12, S =2.
12.4. m =3, t =55, S =5.
12.6. m =5, t =18, S =2.
12.8. m =4, t =10, S =5.
12.10. m =3, t =35, S =7.
12.12. m =2, t =20, S =6.
12.14. m =3, t =15, S =3.
12.16. m =3, t =16, S =4.
12.18. m =3, t =20, S =4.
12.20. m =5, t =16, S =3.
12.22. m =3, t =10, S =3.
12.24. m =4, t =40, S =8.
| 13.1.–13.24. АТС имеет k линий связи. Поток вызовов простейший с интенсивностью λ; вызовов в минуту. Среднее время переговоров составляет t минут. Время переговоров распределено по показательному закону.
Найти абсолютную и относительную пропускные способности АТС, вероятность того, что все линии связи заняты; среднее число занятых линий связи. Определить, сколько линий связей должна иметь АТС, чтобы вероятность отказа не превышала a.
| 13.1. k =3, λ;=0,9, t =2,5, a =0,06.
13.3. k =5, λ;=0,8, t =2,9, a =0,05.
13.5. k =5, λ;=0,7, t =3,5, a =0,05.
13.7. k =3, λ;=0,8, t =2,6, a =0,06.
13.9. k =3, λ;=0,7, t =3,1, a =0,06.
13.11. k =2, λ;=0,5, t =2,3, a =0,07.
13.13. k =3, λ;=0,7, t =3,3, a =0,07.
13.15. k =3, λ;=0,6, t =2,5, a =0,05.
13.17. k =4, λ;=0,8, t =2,5, a =0,03.
13.19. k =4, λ;=0,6, t =3,6, a =0,05.
13.21. k =4, λ;=0,7, t =3,0, a =0,02.
13.23. k =6, λ;=0,6, t =3,5, a =0,08.
| 13.2. k =4, λ;=0,7, t =2,7 a =0,01.
13.4. k =3, λ;=0,6, t =3,5, a =0,06.
13.6. k =4, λ;=0,8, t =2,2, a =0,01.
13.8. k =4, λ;=0,9, t =2,1, a =0,01.
13.10. k =5, λ;=0,9, t =2,8, a =0,05.
13.12. k =4, λ;=0,8, t =2,4, a =0,04.
13.14. k =3, λ;=0,5, t =2,2, a =0,03.
13.16. k =5, λ;=0,8, t =3,6, a =0,08.
13.18. k =4, λ;=0,6, t =3,4, a =0,04.
13.20. k =4, λ;=0,6, t =3,0, a =0,06.
13.22. k =4, λ;=0,6, t =2,4, a =0,07.
13.24. k =3, λ;=0,6, t =3,2, a =0,04.
|
14.1.–14.24. На железнодорожной станции имеется k кассовых аппаратов. Поток пассажиров, желающих приобрести билет, является простейшим с интенсивностью λ; пассажиров в минуту. Время обслуживания распределено по показательному закону. Среднее время обслуживания составляет t секунд.
Определить, существует ли стационарный режим работы железнодорожной кассы; вероятность того, что пассажир застанет все аппараты занятыми; среднее число пассажиров в очереди за билетами; среднее число пассажиров в кассе; среднее время пребывания пассажира в очереди; среднее время пребывания пассажира в кассе.
| 14.1. k =5, λ;=58, t =4,2.
14.3. k =4, λ;=55, t =3,5.
14.5. k =3, λ;=52, t =2,5.
14.7. k =4, λ;=53, t =4,3.
14.9. k =5, λ;=60, t =3,8.
14.11. k =4, λ;=48, t =3,7.
14.13. k =5, λ;=35, t =3,5.
14.15. k =3, λ;=38, t =3,1.
14.17. k =5, λ;=50, t =2,5.
14.19. k =4, λ;=54, t =3,5.
14.21. k =2, λ;=40, t =2,9.
14.23. k =3, λ;=50, t =2,5.
| 14.2. k =3, λ;=62, t =2,2.
14.4. k =5, λ;=50, t =5,1.
14.6. k =3, λ;=58, t =2,8.
14.8. k =4, λ;=54, t =3,3.
14.10. k =3, λ;=55, t =3,1.
14.12. k =6, λ;=52, t =3,9.
14.14. k =3, λ;=52, t =3,0.
14.16. k =5, λ;=68, t =2,5.
14.18. k =4, λ;=57, t =3,7.
14.20. k =3, λ;=50, t =3,0.
14.22. k =4, λ;=28, t =7,0.
14.24. k =4, λ;=59, t =3,6.
|
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|
Условия приобретения статуса индивидуального предпринимателя. В соответствии с п. 1 ст. 23 ГК РФ гражданин вправе заниматься предпринимательской деятельностью без образования юридического лица с момента государственной регистрации в качестве индивидуального предпринимателя. Каковы же условия такой регистрации и...
Седалищно-прямокишечная ямка Седалищно-прямокишечная (анальная) ямка, fossa ischiorectalis (ischioanalis) – это парное углубление в области промежности, находящееся по бокам от конечного отдела прямой кишки и седалищных бугров, заполненное жировой клетчаткой, сосудами, нервами и...
Основные структурные физиотерапевтические подразделения Физиотерапевтическое подразделение является одним из структурных подразделений лечебно-профилактического учреждения, которое предназначено для оказания физиотерапевтической помощи...
|
Способы тактических действий при проведении специальных операций Специальные операции проводятся с применением следующих основных тактических способов действий: охрана...
Искусство подбора персонала. Как оценить человека за час Искусство подбора персонала. Как оценить человека за час...
Этапы творческого процесса в изобразительной деятельности По мнению многих авторов, возникновение творческого начала в детской художественной практике носит такой же поэтапный характер, как и процесс творчества у мастеров искусства...
|
|



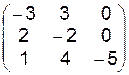


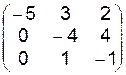
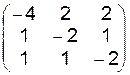

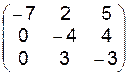
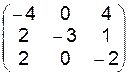

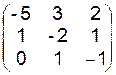

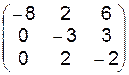


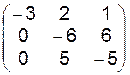




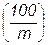 % своей номинальной производительности.
% своей номинальной производительности.


