Answer: B. 160. Impedances 50 Ω and (-j50) Ω are connected in parallel
160. Impedances 50 Ω and (-j50) Ω are connected in parallel. What is their equivalent impedance? A).25-j25 B).25+j25 C).70.71∟- 45° D). 70.71∟45° E). 35∟45° Solution:
Answer: B
161. Define rms value for the function v(t)= 5cos(1000t+30°) A) 10V B) 5V C) 3.5V D) 7V E) –7V Solution:
Answer: C 162. Nano- means multiplication by A)106 B). 10-6 C). 103 D). 10-9 E). 10-12 Answer: D
163. We have known R1, R2, and R3 for star. What is RA for star-to-delta transformation?.
A)RA = (R1 + R2 + R3)/ R1 B). RA = (R1 + R2 + R3)/R2 R1 C) RA = (R1R2 + R2R3+R1R3)/ R2 D) RA = (R1R2 + R2R3+R1R3)/ R3 E) RA = (R1R2 + R2R3+R1R3)/ R1 Solution:
Answer: E
164. Current i is defined as A)dw/dt B). dq/dt C). dw/dq D). dq/dv E). dp/dt Answer: B
165. If the zero-input response of parallel RLC circuit is of underdamped form it has got such view: A)iL(t)=K1e-αtcosβt+K2e-αtsinβt B). iL(t)=K1e-αtcosβt+K2te-αtsinβt. C)iL(t)=K1e-α1t+K2e-α2t D). iL(t)=K1e-α1t+K2te-α2t E). iL(t)=K1e-αt+K2te-αt Answer: A
166. If the zero-input response of parallel RLC circuit is of critically damped form it has got such view: A)iL(t)=K1e-αtcosβt+K2e-αtsinβt B). iL(t)=K1e-αtcosβt+K2te-αtsinβt. C)iL(t)=K1e-α1t+K2e-α2t D). iL(t)=K1e-α1t+K2te-α2t E). iL(t)=K1e-αt+K2te-αt Answer: D
167. Impedances 50 Ω and (-j50) Ω are connected in series. What is their equivalent impedance? A).25-j25 B)25+j25 C)70.71∟- 45° D) 70.71∟45° E) 35∟45° Solution:
Answer: C
168. L=5 mH, ω=106rad/s. Inductive reactance is equal to A)5kΩ; B)j5kΩ C). – j5kΩ D) j500Ω E). – j500Ω Solution:
Answer: A
169. C=5 nF, ω=106rad/s. Capacitive reactance is equal to A)2kΩ B)j2kΩ C) – j2kΩ D) 200Ω; E) – j200Ω Solution:
Answer: D
170. C=5 pF, ω=106rad/s. Impedance is equal to A)200kΩ B)j200kΩ C) – j200kΩ; D) j5000Ω E) – j5000Ω Solution:
|

 , Ω
, Ω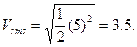 V
V
 .
. 70.71∟-45°.
70.71∟-45°.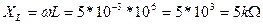 .
. .
. .
.