Рівняння Максвелла
Дж. К. Максвелл записав свої геніальні рівняння в 1865 р. Рівняння Максвелла – це фундаментальні рівняння електродинаміки, які описують електромагнітні явища в будь-якому середовищі. Вони узагальнюють експериментальні і теоретичні праці фізиків першої половини XІX ст. і, насамперед, дослідження М. Фарадея. Основні закони електродинаміки Максвелл сформулював у вигляді чотирьох рівнянь, які подамо в інтегральній формі, як в найбільш простій і наочній. Перше рівняння Максвелла спирається на закон Біо–Савара–Лапласа та поняття струму зміщення. Виділимо в провіднику, в якому існує змінний струм, довільну площадку S, обмежену контуром l. Тоді
де Hl – проекція вектора напруженості магнітного поля на напрям дотичної до контура l у даній точці, jn – нормальна до вибраної площадки складова густини струму провідності, Dn – нормальна до площадки складова вектора електричної індукції. Тут вжита частинна похідна ¶ D /¶ t, щоб врахувати факт залежності D як від часу, так і від просторової координати. Струм зміщення виникає лише тоді, коли D змінюється з часом. Це рівняння показує, що магнітне поле вихрове і що воно виникає незалежно від наявності постійних магнітів. Виникнення магнітного поля зумовлене двома факторами: рухом електричних зарядів (струм провідності) і зміною в часі електричного поля (струм зміщення). Друге рівняння відображає закон електромагнітної індукції Фарадея: eі = ЕРС, як відомо, дорівнює роботі сторонніх сил по переміщенню одиничного заряду, тобто
де El – проекція вектора напруженості електричного поля на напрям дотичної до контура у даній точці, Bn – нормальна до поверхні складова вектора магнітної індукції. З цього рівняння видно, що крім електростатичного поля в природі існує електричне поле, джерелом якого є змінне магнітне поле. Всяка зміна електричного поля зумовлює появу змінного магнітного поля, лінії напруженості якого замкнені і охоплюють лінії електричного поля (перше рівняння); всяка зміна магнітного поля зумовлює появу змінного електричного поля, лінії напруженості якого замкнуті й охоплюють лінії магнітного поля (друге рівняння). Третє рівняння Максвелла показує, що джерелом електричного поля є електричні заряди:
Ліва частина цього рівняння – потік вектора індукції електричного поля через замкнену поверхню площею S. Четверте рівняння відображає факт відсутності магнітних зарядів. Повний потік вектора магнітної індукції В через замкнену поверхню площею S дорівнює нулю:
Наведені рівняння Максвелла не враховують будову речовини і взаємодію електромагнітного поля з частинками речовини. Вплив середовища на електромагнітне поле задається через його електропровідність, а також діелектричну e і магнітну m проникності. Тому до рівнянь Максвелла слід додати ще три рівняння, які називаються матеріальними:
j = s E. Рівняння Максвелла описують величезне коло явищ (електродинаміка, оптика, електротехніка, радіотехніка, астрофізика, фізика плазми тощo). Теорія Максвелла не тільки пояснила вже відомі факти, а й передбачила нові і важливі явища. Абсолютно новим у цій теорії було припущення Максвелла про магнітні поля струмів зміщення. На основі цього припущення Максвелл предбачив існування електромагнітних хвиль, тобто змінного електромагнітного поля, яке поширюється в просторі з певною швидкістю. Теоретичне дослідження властивостей електромагнітних хвиль привело згодом Максвелла до створення електромагнітної теорії світла. Пізніше експериментально вдалося отримати електромагнітні хвилі і провести досліди, які блискуче підтвердили електромагнітну теорію світла, а з нею і всю теорію Максвелла.
|


 , (4.88)
, (4.88) .
. , тому матимемо
, тому матимемо = – ¶ Ф /¶ t ®
= – ¶ Ф /¶ t ®  dS, (4.89)
dS, (4.89) = q.
= q. = 0.
= 0.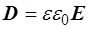 ,
, ,
,


