Аппроксимация функций.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
Кафедра прикладной математики
ЧИСЛЕННЫЕ МЕТОДЫ
Часть 2
Методические указания к лабораторным и самостоятельным работам по курсам «Информатика» и «Вычислительная математика»
Казань
УДК 621.313: 518.6 ББК 32.81
А95 Численные методы. Часть 2: Методические указания к лабораторным и самостоятельным работам по курсам «Информатика» и «Вычислительная математика». / Сост.: Ф.Г.Ахмадиев, Ф.Г.Габбасов, Р.Ф.Гиззятов, И.В.Маланичев. – Казань: Изд-во Казанск. гос. архитект.-строит. ун-та, 2013. – 36 с.
Печатается по решению Редакционно-издательского совета Казанского государственного архитектурно-строительного университета.
Методические указания состоят из двух частей и предназначены для выполнения лабораторных и самостоятельных работ студентами всех специальностей и направлений подготовки дневного и заочного отделений. В данной части приводятся численные методы аппроксимации функций, вычисления определенных интегралов, решения дифференциальных уравнений и задач линейного программирования.
Рецензент Доктор физико-математических наук, профессор КГАСУ Р.Б.Салимов
УДК 621.313: 518.6 ББК 32.81
Очень часто в практической работе возникает необходимость найти в явном виде функциональную зависимость (формулу) Задача восстановления аналитической функции по отдельным значениям называется аппроксимацией. Для получения единственного решения задачи аппроксимации необходимо 1. Задать общий вид аппроксимирующей функции, включающий неизвестные параметры (коэффициенты). Вид функции задается, исходя из формы распределения аппроксимируемых значений (расположения точек на графике), из предполагаемой функциональной зависимости, или просто в виде полинома некоторой степени; 2. Определить значения параметров на основе заданного критерия близости. Здесь существует два основных подхода – интерполяция и сглаживание. 4.1. Интерполяция.
 к исходным данным к исходным данным  , ,  рассматривается как совпадение значений в заданных точках, называемых узлами интерполяции (рис. 4.1), т.е. рассматривается как совпадение значений в заданных точках, называемых узлами интерполяции (рис. 4.1), т.е.
Если функция задана в виде полинома, то он называется интерполяционным полиномом и может быть записан, например, в форме Лагранжа или Ньютона. 4.1.1. Интерполяционный полином в форме Лагранжа. Пусть на некотором промежутке
Интерполяционный полином Лагранжа имеет следующую формулу:
где
и зависят лишь от заданных узлов Пример 4.1. Пусть задана таблица:
Решение. Полином Лагранжа имеет вид:
Найдем фундаментальные полиномы Лагранжа:
Подставляя
|

 и
и  , которые заданы отдельными парами значений
, которые заданы отдельными парами значений 
 .
.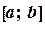 заданы
заданы  различных узлов
различных узлов  ,
, 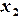 ,
,  , …,
, …,  , а также значения некоторой функции
, а также значения некоторой функции  ,
,  ,
,  , …,
, …,  в этих узлах. Необходимо построить полином
в этих узлах. Необходимо построить полином  , проходящий через заданные точки, т.е.
, проходящий через заданные точки, т.е.
 (4.1)
(4.1) - фундаментальные полиномы Лагранжа. Они удовлетворяют равенствам
- фундаментальные полиномы Лагранжа. Они удовлетворяют равенствам (4.2)
(4.2)








 в полином Лагранжа, находим:
в полином Лагранжа, находим:



