Оценка точности вычисления определенного интеграла.
Погрешность вычисления значения интеграла
где
Таким образом, интеграл вычисляется по выбранной формуле (прямоугольников, трапеций, парабол Симпсона) для последовательных значений числа шагов Пример 5.1. Вычислить определенный интеграл методами прямоугольников, трапеций и парабол:
Решение. Выберем на отрезке интегрирования
Шаг разбиения для равноотстоящих узлов определяем по формуле
Сравнивая формулы 5.4, 5.5, 5.13 и 5.16, обратим внимание, что определенный интеграл приближенно можно вычислять по формуле
где
Вычислим значения функции в узлах (табл. 5.3). Таблица 5.3
Вычислим интеграл: По формуле левых прямоугольников
По формуле правых прямоугольников
По формуле трапеций
По формуле парабол
Пример 5.2. Вычислить с помощью программы Excel определенный интеграл методом трапеций
|
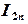при числе шагов 
, равном 
, определяется по формуле Рунге:
- значения интеграла при числе шагов, равном 
,
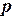- порядок точности, равный 
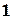для формулы левых (правых) прямоугольников, 2 для формулы трапеций и 4 для формулы Симпсона.
, 
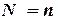, и т.д. Процесс вычислений заканчивается, когда для очередного значения 
будет выполнено условие 
, где ε; ‑ заданная точность.
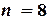различных узлов
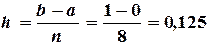
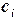- числовые коэффициенты, на которые умножаются значения функции в узлах 
:
- для метода левых прямоугольников;
- для метода правых прямоугольников;
- для метода трапеций;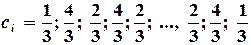
- для метода парабол
