Порядок решения. 1) Аппроксимирующая функция должна иметь экстремум в виде пика
1) Аппроксимирующая функция должна иметь экстремум в виде пика. Выберем следующую функцию, зависящую от трех параметров 2) Ввести в ячейки A2, B2, C2 (рис. 4.7) начальные значения параметров 3) В ячейки A5:A11 – значения 4) В ячейки B5:B11 – значения 5) В ячейку C5 – формулу аппроксимирующей функции (на ячейки с параметрами абсолютные ссылки): =$A$2*EXP(-((A5-$B$2)^2)/$C$2) 6) Скопировать формулу в ячейки C6:C11 7) В ячейку D5 – формулу квадрата разности: =(B5-C5)^2 8) Скопировать формулу в ячейки D6:D11 9) В ячейку D12 – сумму квадратов: =СУММ(D5:D11) 10) Вызвать окно Поиск решения. В настройках указать: Установить целевую ячейку $D$12 Равной минимальному значению Изменяя ячейки $A$2:$C$2 11) Нажать кнопку Выполнить. 12) Подтвердить сохранение найденного решения. 13) Рабочий лист изменился и содержит решение (рис. 4.5):
Таким образом, аппроксимирующая данные табл. 4.11 функция имеет вид:
Точность аппроксимации можно оценить среднеквадратической ошибкой
которая не должна превышать погрешность исходных данных (рис. 4.3а).
|

 :
: 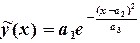 ;
;






 ,
,


