Разностные методы решения краевой задачи для обыкновенного дифференциального уравнения.
Линейная краевая задача имеет вид:
при Решение задачи (6.9)-(6.10) проводится в следующей последовательности: 1. Определение сетки. Отрезок [a,b] делится на
2. Определение сеточной функции
3. Аппроксимация уравнения: Для каждой узловой точки
Получаем ситему 4. Решение СЛАУ. Система Пример 6.4. Решить краевую задачу методом конечных разностей с шагом
Решение. Решение проводим в следующей последовательности: 1. Определение сетки:
2. Определение сеточной функции
3. Аппроксимация уравнения:
Получим систему четырех линейных алгебраическихуравнений с четырьмя неизвестными
или
4. Решение системы методом прогонки. Значения
Прямой ход прогонки. Определяем прогоночные коэффициенты
Обратный ход прогонки. Вычисляем Поскольку
Сеточную функцию
|
(6.9)
(6.10)
.
частей:
, 
, 
:
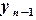
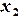
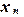
заменяем функции и производные в уравнениях 6.9-6.10 конечноразностными аналогами:
т.е. 
(6.11)
т.е. 
линейных алгебраических уравнений для определения 
:
| | | |
, 
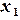- краевые точки, 
- внутренние точки.
, 
, 
, 
записываем в виде таблицы.
и 
(
).
, т.к. 
).
, то 
.
