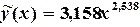Порядок решения.
1) Ввести таблицу в рабочий лист Excel (рис. 4.4). Выделить ячейки таблицы. 2) Вставить диаграмму: Вставка – Диаграммы – Точечная – точечная с маркерами. На рабочем листе появится график точек таблицы.
3) Вызвать контекстное меню (правой кнопкой мыши) одной из точек графика. Выбрать пункт «Добавить линию тренда». 4) Выбрать «Полиномиальная№ аппроксимация и установить степень полинома, равной 2 (рис. 4.5). 5) Отметить «показывать уравнение на диаграмме».
6) Закрыть окно настроек. Появляется линия графика аппроксимирующей функции и соответствующая формула (рис. 4.6):
Аппроксимация линеаризацией. Многие нелинейные функции, зависящие от двух параметров, можно линеаризовать путем замены переменных. Для этого необходимо подобрать такое преобразование исходной зависимости
Пример 4.7. Используя МНК, построить функцию вида
Решение. Расчеты представим в виде таблицы.
Система для определения коэффициентов имеет вид:
Решая систему (4.12), получим следующие значения параметров: Тогда (табл. 4.8) Аппроксимирующая функция имеет вид:
Аппроксимация произвольной функцией может быть выполнена в программе Excel с помощью модуля «Поиск решения». Пример 4.8. Используя программу Excel, построить функцию, аппроксимирующую значения из таблицы:
|





 , в результате которого она приобретает линейный вид
, в результате которого она приобретает линейный вид  . Далее решается задача линейной аппроксимации для новой зависимости, и вычисленные коэффициенты
. Далее решается задача линейной аппроксимации для новой зависимости, и вычисленные коэффициенты 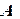 и
и  пересчитываются в
пересчитываются в  и
и  .
.



















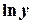



 , аппроксимирующую следующие табличные значения:
, аппроксимирующую следующие табличные значения:


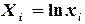





 (4.12)
(4.12) ,
,  .
. ,
,  .
.