Свойства функции F(x) (самостоятельно)
Доказательство: Так как по определению F(x) - это вероятность Р(Х<х), а вероятность всегда есть число неотрицательное, не превышающее 1.
Доказательство: Рассмотрим событие Х<х2. Оно может быть представлено в виде суммы двух несовместных событий, т.е. (или Х<х1, или х1£Х<х2).
х1£Х<х2 Применим теорему сложения вероятностей для несовместных событий. Р (Х<х2)= Р (Х<х1)+ Р (х1£Х<х2) отсюда Р (Х<х2)-Р (Х<х1)=Р (х1£Х<х2) или F(x2) -F(x1) = Р (х1£Х<х2) (*) Так как любая вероятность есть число неотрицательное, то: F(x2) -F(x1)³ 0 или F(x2) ³ F(x1). Следствие 1. Вероятность попадания СВ Х в заданный интервал.
Это следует из равенства (*) при Х1 = a Х2= b. Следствие 2
Доказательство: Пусть Х- непрерывная СВ. Рассмотрим формулу 7 следствия 1: Р(a £ Х<b) = F(b)- F(a). Пусть a=х1, а b= х1+ Dх. Тогда Р(х1 £ Х < х1+ Dх)= F(x1+ Dх) -F(x1). Пусть Dх®0. Так как Х- непрерывная СВ, то функция F(x)- непрерывная. В силу непрерывности F(x) в точке х1 разность F(x1+ Dх) -F(x1) будет ®0 и, следовательно, В принципе, для дискретной СВ можно указать вероятность появления каждого ее значения, а для непрерывной СВ это сделать нельзя. Допустим, требуется определить вероятность того, что расход топлива на 100 километров пути составит точно 12 литров. Однако в зависимости от типа трассы, технического состояния автомобиля, качества топлива и многих других факторов расход горючего абсолютно точно измерить нельзя. Количество бензина, расходуемого на 100 км. пути от заправки к заправке будет немного меняться. Вероятность того, что это будет точно 12 литров практически равна нулю. Р(Х) =0 Используя это положение, убедимся в справедливости равенства. Р(a £ Х<b)= Р(a < Х<b) = Р(a<Х£ b) = Р(a £ Х£ b) (9) Например, докажем, что: 1) Р(a<Х£ b)= Р(a < Х<b) Р(a<Х£ b) = Р(a < Х<b) + Р (Х=b=0) = Р(a < Х<b) 2) Р(a £ Х<b) = Р(х=a =0)+ Р(a < Х<b)= Р(a < Х<b). При определении вероятности того, что НСВ попадет в интервал, можно не делать различия между случаями, когда концы интервала принадлежат или н принадлежат интервалу.
интервал возможных значений Пусть СВ Х<a, тогда событие (Х<х)=Æ, т.е. Р(Х<х)= F(x) =0. Пусть СВ Х> b, тогда событие (Х<х)=W и Р(Х<х)= F(x) = 1. Следствие:
или F(-¥)= 0, (10’) так как событие (Х<-¥) = Æ и F(+¥)=1, (10”) Так как событие (Х<+¥)=W.
Доказательство: События (Х³х) и (Х<х)- противоположные, поэтому Р (Х³х)+ Р(Х<х)=1 Р (Х³х) =1- Р(Х<х), т.е. Р (Х³х) =1- F(x)
|


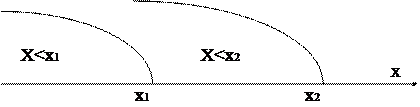
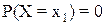 (8)
(8)
 [F(x1+ Dх) -F(x1)]=0; а
[F(x1+ Dх) -F(x1)]=0; а 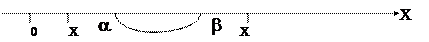

 Доказательство:
Доказательство: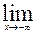 F(x) =0;
F(x) =0; 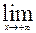 F(x) =1
F(x) =1