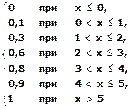Или интегральный закон распределения)
Задание закона распределения СВ в виде ряда распределения не всегда приемлемо, потому что для НСВ множество её возможных значений бесконечно и сплошь заполняет некоторый промежуток. Кроме того, как будет показано в дальнейшем для НСВ Р(Х=х)=0, то есть отдельное значение НСВ обладает нулевой вероятностью. Это означает, что все значения НСВ, образующие бесконечное множество, имеют одинаковую и равную нулю вероятность. Как быть? Несмотря на равенство нулю отдельных значений НСВ, можно находить вероятности её значений в различных интервалах, в которых она обладает различными и отличными от нуля вероятностями. Таким образом, для НСВ также можно определить закон распределения вероятностей, но в ином, чем для ДСВ виде. Для количественной характеристики распределения НСВ Х рассматривают не вероятность события (Х=х), а вероятность события (Х<х), где х - произвольное действительное число (т.к. Р(Х=х)=0, но это будет доказано позже). Для нас представляет интерес вероятность события, состоящего в том, что в результате опыта СВ Х приняла значение, которое оказалось меньше фиксированного х. Если х изменяется произвольно, то и вероятность выполнения неравенства Х<x в общем случае будет изменяться. Следовательно, вероятность Р(Х<x) является функцией аргумента х. Обозначим эту функцию как F(x).
F(x) - есть вероятность того, что случайная точка Х окажется левее фиксируемой точки. Итак, СВ Х можно рассматривать как случайную точку на числовой оси. Пусть на оси выбрана конкретная точка х, тогда в результате опыта случайная точка Х может оказаться левее или правее выбранной нами точки. Очевидно, что вероятность того, что случайная точка Х окажется левее точки х будет зависеть от положения точки х, то есть являться функцией аргумента х. Для ДСВ Х, которая может принимать значения х1, х2,...,хn, функция распределения примет вид
Где неравенство хi<x под знаком суммы означает, что суммирование касается тех значений хi, величина которых меньше х. Поясним эту формулу, исходя из определения F(x). Предположим, что аргумент х принял какое-то определенное значение, но такое, что выполняется неравенство Функция распределения (интегральная функция распределения) существует как для дискретных, так и для непрерывных СВ. F(х) является универсальной формой закона распределения.
Построим функцию распределения, ряд которой представлен в (2), то есть
Для примера 1 построим функцию распределения случайной величины Х - числа рекламных объявлений.
Случайная величина Х не принимает значений, меньших 0. Следовательно, если х При х £ 0 имеем F(x) =0, т.к. F(x)= Р (х<0)=0; При 0<х £1 имеем F(x) = Р (х<1)=Р (х=0)=0,1; При 1<х£2 имеем F(x) = Р (х<2)=Р(или 0, или 1)=Р(х=0)+ Р(х=1)=0,1+0,2=0,3; При 2<х£3 имеем F(x) = Р (х<3)=Р(или 0, или 1, или 2)= 0,1+0,2+0,3=0,6. При 3<х£4 имеем F(x) = Р (х<4)=Р(или 0, или 1, или 2, или 3)= 0,1+0,2+0,3+0,2=0,8. При 4<х£5 имеем F(x) = Р (х<5)=Р(или 0, или 1, или 2, или 3, или 4)= 0,1+0,2+0,3+0,2+0,1=0,9. При х>5 F(x) =Р (х>5)= Р(или 0, или 1, или 2, или 3, или 4, или 5)= 0,1+0,2+0,3+0,2+0,1+0,1=1,0.
Запишем ее в табличной форме. Таблица 3 Функция распределения (интегральная функция распределения) для примера 3
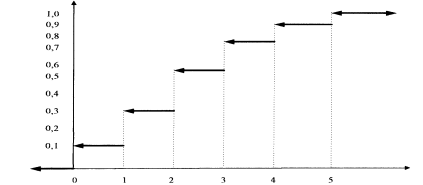
или F(x) можно аналитически записать так: F(x)= Изобразим график построенной функции:
Рис2 Рис.2 показывает, что интегральная функция - неубывающая и равна единице при х большем наибольшего возможного значения случайной величины. В нашем примере график F(x) имеет ступенчатый вид. Для ДСВ график представляет собой разрывную ступенчатую линию. Когда переменная Х проходит через какое-либо из возможных значений СВ, значение функции распределения меняется скачкообразно, то есть функция имеет скачок в тех точках, в которых СВ принимает конкретное значение согласно ряду распределения, причем величина скачка равна вероятности этого значения. Сумма величин всех скачков равна 1. В интервалах между значениями СВ функция F(x) постоянна.
|

 геометрически:
геометрически:
 (5)
(5) . Тогда левее числа х на числовой оси окажутся только те значения, которые имеют индекс 1,2,3,… ,i. Поэтому неравенство X<x выполняется, если величина Х примет значение xk , где k=1,2,3,…,i. Таким образом, событие X<x наступит, если наступит любое, неважно какое, из событий X=x1, X=x2, X=x3, …, X=xi. Так как эти события несовместные, то по теореме сложения вероятностей имеем
. Тогда левее числа х на числовой оси окажутся только те значения, которые имеют индекс 1,2,3,… ,i. Поэтому неравенство X<x выполняется, если величина Х примет значение xk , где k=1,2,3,…,i. Таким образом, событие X<x наступит, если наступит любое, неважно какое, из событий X=x1, X=x2, X=x3, …, X=xi. Так как эти события несовместные, то по теореме сложения вероятностей имеем 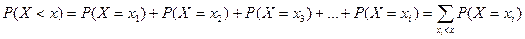 .
.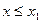
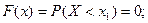

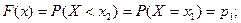
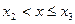


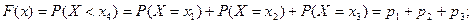
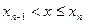


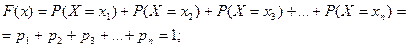
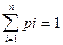 )
)
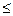 0, то событие Х < х - невозможно, а вероятность его равна нулю. Поэтому функция распределения случайной величины Х для всех значений х
0, то событие Х < х - невозможно, а вероятность его равна нулю. Поэтому функция распределения случайной величины Х для всех значений х  1
1