Ряд распределения СВ
Ряд распределения - это простейшая форма закона распределения. Он существует только для дискретных СВ.
Таким образом, СВ Х в результате испытание может принять одно из возможных значений х1, х2,... хn с вероятностями Р(Х= x1)= р1, Р (Х= х2)= р2,..., Р(Х= хn)= рn. Например, запись P(X=5) = 0,2 означает, что вероятность того, что случайная величина Х примет значение, равное 5, есть 0,2. Можно также использовать более короткую запись: P(x) вместо P(X=x), или P(5) = 0,2. Так как события (Х= x1), (Х= х2),...,(Х= хn) составляют полную группу событий, то сумма вероятностей р1, р2,....., рn равна единице:
(3)
Пример 1. Каждый день местная газета получает заказы на новые рекламные объявления, которые будут напечатаны на следующий день. Число рекламных объявлений в газете зависит от многих факторов: дня недели, сезона, общего состояния экономики, активности местного бизнеса и т.д. Пусть Х - число новых рекламных объявлений, напечатанных в местной газете в определенный день. Х - СВ, которая может быть только целым числом. Пусть, например, СВ Х принимает значения 0, 1, 2, 3, 4, 5 с вероятностями 0,1; 0,2; 0,3; 0,2; 0,1; 0,1 соответственно. Таблица 1 Ряд распределения случайной величины Х числа рекламных объявлений
Из таблицы 1 следует, что вероятность того, что в определенный день будут напечатаны 3 объявления, равна 0,2, а 2 объявления - 0,3 и т.д. Поскольку появления различных значений случайной величины Х - несовместные события, то вероятность того, что в газету будут помещены или 2 или 3 рекламных объявления, - равна сумме вероятностей Р(2) + Р(3) = 0,3 +0,2 = 0,5. Вероятность же того, что их число будет находиться в пределах от 1 до 4 (включая 1 и 4), равна 0,8, то есть Р(1 Ряд распределения можно изобразить графически. Для этого по оси абсцисс откладывают возможные значения СВ, а на оси ординат- их соответствующие вероятности. Точки (хi, рi) соединяют отрезками прямых.
Рис.1.
|

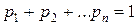
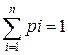
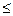 Х
Х 



