Случайной величины
1. Математическое ожидание постоянной величины равно этой постоянной М(с) = с (13)
2. Постоянный множитель можно выносить за знак математического ожидания, то есть
где с - постоянная величина
М(Х1±X2± ×××±Xn) = М(Х1) ± М(X2) ± ×××± M(Xn) (15)
4. Математическое ожидание произведения конечного числа n независимых случайных величин равно произведению их математических ожиданий, то есть
5. Если все значения случайной величины Х уменьшить (увеличить) на одно и то же число с, то ее математическое ожидание уменьшится (увеличится) на то же число с, то есть
М[Х - М(Х)] = 0 (18)
М(X) = М(Х i ) (19) Пусть Х1 , Х2,..., Х n - одинаково распределенные случайные величины, математические ожидания каждой из которых одинаковы и равны M(X) = 1/n× M(X1 + X2 +... + Xn) = n M(X) = a Пример 6. В книжном магазине организована лотерея. Разыгрываются две книги стоимостью по 10 рублей и одна - стоимостью в 30 рублей. Составьте закон распределения суммы выигрыша для посетителя магазина, который приобрел два билета стоимостью по 1 руб, а также найдите математическое ожидание суммы выигрыша и убедитесь в справедливости формулы М(Х+У) = М(Х) + М(У). Сумма выигрыша на первый и второй билеты лотереи с учетом затрат на их приобретение являются случайными величинами, которые обозначим соответственно Х и У. Это одинаково распределенные случайные величины. Сумма выигрыша для посетителя, который приобрел два билета, является случайной величиной. Она представляет собой сумму случайных величин Х и У, которые являются зависимыми. Для нахождения закона распределения случайной величины Х + У рассмотрим различные возможные исходы лотереи. Расчеты оформим в следующей таблице. Таблица 5
При нахождении вероятностей соответствующих результатов применяется теорема умножения вероятностей для зависимых событий. Например, случайная величина Х+У примет значение - 2 руб., если покупатель не выиграет ни на первый билет, ни на второй билет. Вероятность не выиграть на первый билет лотереи равна По теореме умножения получаем вероятность не выиграть на оба билета. Вероятность выиграть на оба билета книги по 30 руб оказывается равной 0, так как имеется лишь один такой выигрыш. Таким образом, случайная величина Х+У может принимать следующие значения: -2, 8, 18, 28 и 38 руб. Ее закон распределения имеет вид:
Вероятности Р(Х+У=8), Р(Х+У=28) и Р(Х+У = 38) получаем, используя теорему сложения вероятностей. Найдем математическое ожидание Х+У: М(Х+У) =(-2) М(Х)=М(У) =-1 × 0,94+9×0,04+29×0,02=(-1)× Следовательно, М(Х+У) = М(Х) + М(У)
|

 М(сХ) = сМ(Х) (14)
М(сХ) = сМ(Х) (14) 3. Математическое ожидание алгебраической суммы конечного числа n случайных величин равно алгебраической сумме их математических ожиданий, то есть
3. Математическое ожидание алгебраической суммы конечного числа n случайных величин равно алгебраической сумме их математических ожиданий, то есть М(Х1 ×X2 ×××Xn) = М(Х1) × М(X2) ××× M(Xn) (16)
М(Х1 ×X2 ×××Xn) = М(Х1) × М(X2) ××× M(Xn) (16) М(Х - С) = М(Х) - С (17)
М(Х - С) = М(Х) - С (17) Следствие. Математическое ожидание отклонений значений случайной величины Х от ее математического ожидания равно нулю, то есть
Следствие. Математическое ожидание отклонений значений случайной величины Х от ее математического ожидания равно нулю, то есть 6. Математическое ожидание среднего арифметического значения n одинаково распределенных взаимно независимых [1] случайных величин равно математическому ожиданию каждой из величин, то есть
6. Математическое ожидание среднего арифметического значения n одинаково распределенных взаимно независимых [1] случайных величин равно математическому ожиданию каждой из величин, то есть . Тогда математическое ожидание их суммы равно n×
. Тогда математическое ожидание их суммы равно n×  ·
·  =
= 
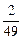 =
= 
 =
= 
 ·
·  =
= 
 ·
·  = 0
= 0
 , на второй при условии, что первый билет не выиграл, -
, на второй при условии, что первый билет не выиграл, -  +18
+18  =0
=0


