Закон распределения СВ
Появление тех или иных значений СВ можно рассматривать как события, а различным событиям в общем случае соответствуют различные вероятности. Поэтому возможные значения СВ отличаются между собой с вероятностной точки зрения. Например, при бросании двух игральных кубиков такие значения СВ Z=X+Y как z=2 и z=8 находятся в «неодинаковых условиях». Значение z=2 может появиться только в одном случае, когда x1 =1и y1=1, а значение z=8 может появиться в пяти случаях. Отсюда следует, что вероятность появления z=2 меньше, чем вероятность появления z=8. Таким образом, перечисление всех возможных значений СВ не дает достаточно полного представления о ней. Кроме того, необходимо знать как часто могут появляться те или иные её значения в результате испытаний, проводящихся в одинаковых условиях, т.е. надо знать вероятности их появления. Рассмотрим ДСВ Х с возможными значениями Х=х1, Х=х2, Х=х3,…, Х=хn В результате опыта СВ примет одно и только одно из этих значений. Другими словами, произойдет одно из несовместных событий, образующих полную группу: Х=х1, Х=х2, Х=х3,…, Х=хn. Обозначим вероятность этих событий буквами р с соответствующими индексами: Р (Х=х1)=р1, Р(Х=х2)=р2, Р(Х=х3)=р3,…, Р(Х=хn)=рn. Так как указанные события образуют полную группу, то сумма вероятностей появления возможных значений СВ =1, т.е.
Если же множество значений СВ образует бесконечное, но счетное множество, то ряд Таким образом, суммарная вероятность распределена между всеми значениями СВ. Определив все возможные значения СВ Х и правило, по которому каждому событию Х=х1, Х=х2, Х=х3,…, Х=хn ставится в соответствие вероятность, то есть правило распределения вероятностей между значениями СВ по которому можно получить полное представление о СВ.
При помощи закона распределения можно определить: 1) вероятность того, что в результате испытания СВ примет одно из возможных своих значений; 2) вероятность того, что СВ окажется меньше или больше некоторого заданного числа; 3) вероятность попадания СВ на заданный интервал; 4) значения различных числовых характеристик СВ. Примеры СВ
Закон распределения СВ может иметь разные формы: ряд распределения, функция распределения, плотность распределения.
|

 (1)
(1)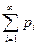 сходится и его сумма равна 1.
сходится и его сумма равна 1.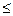 х
х 


