Аксіоми статики
В основі статики лежить ряд аксіом, що являють собою результат узагальнень численних дослідів і спостережень за рівновагою і рухом тіл, неодноразово підтверджених практикою. Аксіоми статики є вихідними положеннями дослідного характеру, що приймаються без доведення. Вони формулюються так.
У механіці така система сил має назву “двійка сил”. Ця аксіома визначає найпростішу зрівноважену систему двох сил, оскільки досліди свідчать, що вільне тіло, на яке діє тільки одна сила, знаходитися в рівновазі не може. Аксіома 2. Дія заданої системи сил на абсолютно тверде тіло не порушується, якщо до неї додати або відняти зрівноважену систему сил (наприклад, двійку сил). Наслідок з аксіоми 2. Не порушуючи стану абсолютно твердого тіла, точку прикладання сили можна переносити вздовж її лінії дії. Доведення. Нехай на абсолютно тверде тіло діє сила
сила Аксіома 3 (аксіома про паралелограм сил). Система двох сил, прикладених в одній точці до абсолютно твердого тіла, має рівнодійну, яка зображується діагоналлю паралелограма, побудованого на цих силах, і прикладена в тій самій точці (рис. 1.5).
сформулювати ще так: дві сили, які прикладені до абсолютно твердого тіла в одній точці, мають рівнодійну, що дорівнює геометричній (векторній) сумі цих сил і прикладена в тій самій точці.
|

 у рівновазі тоді й тільки тоді, коли ці сили рівні за модулем
у рівновазі тоді й тільки тоді, коли ці сили рівні за модулем  і діють уздовж однієї прямої аа у протилежних напрямах (рис. 1.3):
і діють уздовж однієї прямої аа у протилежних напрямах (рис. 1.3):
 .
.



 , прикладена в точці А (рис. 1.4). Візьмемо на лінії дії аа цієї сили довільну точку В і прикладемо в ній дві сили
, прикладена в точці А (рис. 1.4). Візьмемо на лінії дії аа цієї сили довільну точку В і прикладемо в ній дві сили 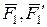 (двійку сил), що дорівнюють за величиною силі
(двійку сил), що дорівнюють за величиною силі  .
. , прикладена в точці В, складають, за побудовою, зрівноважену систему сил. Тому її можна відкинути, не порушуючи стану рівноваги тіла. Отже, залишається
, прикладена в точці В, складають, за побудовою, зрівноважену систему сил. Тому її можна відкинути, не порушуючи стану рівноваги тіла. Отже, залишається





 , яка прикладена в точці В і дорівнює за величиною початковій силі
, яка прикладена в точці В і дорівнює за величиною початковій силі 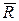 , який дорівнює діагоналі паралелограма, побудованого на векторах
, який дорівнює діагоналі паралелограма, побудованого на векторах  . (1.1)
У цій аксіомі сформульовано правило векторного додавання сил. Тому її можна
. (1.1)
У цій аксіомі сформульовано правило векторного додавання сил. Тому її можна






 Рис. 1.5
Рис. 1.5



