Момент сили відносно точки
Силовий фактор, під дією якого тіло може здійснювати обертальний рух, називається моментом сили відносно точки (полюса). Це фізичне поняття. З математичної точки зору момент сили
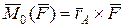 . (4.1) . (4.1)
Рис. 4.1 Отже, враховуючи поняття і визначення векторної алгебри, отримаємо наступні властивості моменту сили відносно точки: - момент сили відносно точки О є зв’язаним у точці вектором, який напрямлений перпендикулярно до площини S, що проходить через точку О і лінію дії а-а сили - в координатній формі момент сили обчислюється так:
де - основною одиницею вимірювання моменту сили відносно точки є 1 Н×м; - за величиною момент сили дорівнює модулю вектора
або де - відповідно до формули (4.3) момент сили відносно полюса дорівнює нулю, якщо лінія дії сили проходить через даний полюс (при цьому плече сили - момент сили відносно точки умовимося вважати додатним (вектор
а) б) Рис. 4.2
|

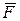 відносно точки О (рис. 4.1) визначається вектором
відносно точки О (рис. 4.1) визначається вектором 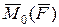 , який дорівнює векторному добутку радіуса-вектора
, який дорівнює векторному добутку радіуса-вектора  точки А прикладання сили на її вектор
точки А прикладання сили на її вектор 
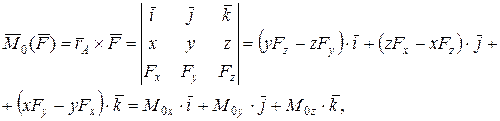 (4.2)
(4.2) ;
; 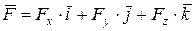 ; M 0 х ; M 0 y; M 0 z – проекції моменту сили відносно точки О на осі системи координат (рис. 4.1);
; M 0 х ; M 0 y; M 0 z – проекції моменту сили відносно точки О на осі системи координат (рис. 4.1);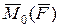 :
: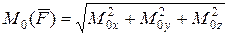 ,
,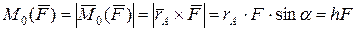 , (4.3)
, (4.3) - плече сили
- плече сили  );
);



