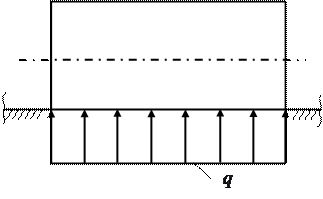
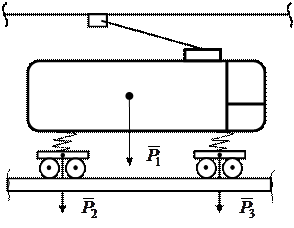
Прикладами паралельних сил є сили ваги вузлів машини, трамваю (рис. 4.5,а), реакції поверхні шляху на коток (рис. 4.5,б) та ін.
|
а
|
 б
б
|
Рис. 4.5
Складання двох сил, напрямлених в один бік
Розглянемо тверде тіло, на яке в точках А і В діють дві паралельні сили  і
і 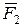 (рис. 4.6). Приведемо вихідну систему паралельних сил до еквівалентної системи збіжних сил
(рис. 4.6). Приведемо вихідну систему паралельних сил до еквівалентної системи збіжних сил  і
і 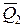 . для цього прикладемо в точках А і В дві зрівноважені, довільні за величиною сили
. для цього прикладемо в точках А і В дві зрівноважені, довільні за величиною сили 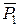 і
і 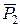 = -
= - 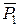 ) і складемо їх за правилом паралелограма. Одержані сили
) і складемо їх за правилом паралелограма. Одержані сили  і
і 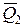 перенесемо до точки О перетину їх ліній дії. Після цього кожну з сил
перенесемо до точки О перетину їх ліній дії. Після цього кожну з сил  і
і 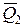 розкладемо на дві складові, кожна з яких дорівнює аналогічним складовим сил
розкладемо на дві складові, кожна з яких дорівнює аналогічним складовим сил  і
і 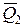 у точках А і В. За побудовою і визначенням отримані складові сили
у точках А і В. За побудовою і визначенням отримані складові сили 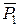 і
і 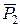 складуть двійку сил, тому їх можна відкинути (закреслено на рис. 4.6). Залишені сили
складуть двійку сил, тому їх можна відкинути (закреслено на рис. 4.6). Залишені сили  і
і 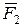 , за побудовою, будуть мати загальну лінію дії. Тому перенесемо їх у точку С перетину зазначеної лінії дії з відрізком АВ. У точці С їх складемо і замінемо рівнодійною:
, за побудовою, будуть мати загальну лінію дії. Тому перенесемо їх у точку С перетину зазначеної лінії дії з відрізком АВ. У точці С їх складемо і замінемо рівнодійною:
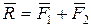 .
.
Для визначення положення точки С на відрізку АВ розглянемо трикутники ОАС, Oak, OВС, Obm. Вони подібні за побудовою, тому будуть виконуватись наступні пропорційні співвідношення їх сторін:
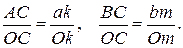 (4.4)
(4.4)
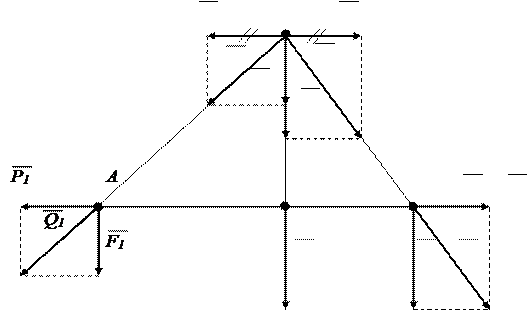 P1 O P2
P1 O P2
Q1 Q2
F1
а k F2
m b
C B P2 = - P 1
R F2 Q2
Рис. 4.6
Розв’язавши пропорції (4.4) та враховуючи, що 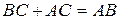 , а
, а 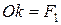 ,
,  , одержимо
, одержимо
 ;
;  ;
; 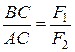 . (4.5)
. (4.5)
У результаті виконаних перетворень початкову систему паралельних сил  ,
, 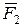 зведено до однієї сили рівнодійної
зведено до однієї сили рівнодійної 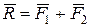 . Отримано також, що рівнодійна двох паралельних сил, які спрямовані в один бік, дорівнює за модулем сумі модулей складових сил, їм паралельна і напрямлена у той же бік; лінія дії рівнодійної проходить між точками прикладання складових сил на відстані від цих точок, обернено пропорційній (4.5) силам.
. Отримано також, що рівнодійна двох паралельних сил, які спрямовані в один бік, дорівнює за модулем сумі модулей складових сил, їм паралельна і напрямлена у той же бік; лінія дії рівнодійної проходить між точками прикладання складових сил на відстані від цих точок, обернено пропорційній (4.5) силам.

 б
б
 і
і 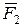 (рис. 4.6). Приведемо вихідну систему паралельних сил до еквівалентної системи збіжних сил
(рис. 4.6). Приведемо вихідну систему паралельних сил до еквівалентної системи збіжних сил  і
і 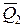 . для цього прикладемо в точках А і В дві зрівноважені, довільні за величиною сили
. для цього прикладемо в точках А і В дві зрівноважені, довільні за величиною сили 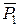 і
і 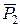 = -
= - 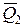 перенесемо до точки О перетину їх ліній дії. Після цього кожну з сил
перенесемо до точки О перетину їх ліній дії. Після цього кожну з сил 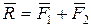 .
.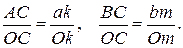 (4.4)
(4.4)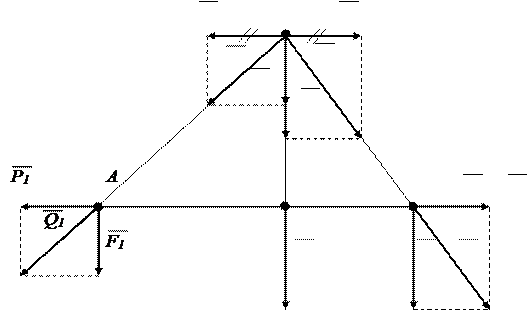 P1 O P2
P1 O P2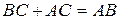 , а
, а 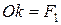 ,
,  , одержимо
, одержимо ;
;  ;
; 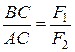 . (4.5)
. (4.5)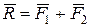 . Отримано також, що рівнодійна двох паралельних сил, які спрямовані в один бік, дорівнює за модулем сумі модулей складових сил, їм паралельна і напрямлена у той же бік; лінія дії рівнодійної проходить між точками прикладання складових сил на відстані від цих точок, обернено пропорційній (4.5) силам.
. Отримано також, що рівнодійна двох паралельних сил, які спрямовані в один бік, дорівнює за модулем сумі модулей складових сил, їм паралельна і напрямлена у той же бік; лінія дії рівнодійної проходить між точками прикладання складових сил на відстані від цих точок, обернено пропорційній (4.5) силам.


