Складання двох сил, напрямлених в різні боки
Зобразимо прикладені до тіла у точках А, В сили
отже, складаючи сили
Рис. 4.7 | Таким чином, рівнодійна двох напрямлених в різні боки паралельних сил дорівнює за величиною різниці модулей заданих сил, їм паралельна і направлена в бік більшої з сил; лінія дії рівнодійної проходить поза відрізком, який з’єднує точки прикладання складових сил, на відстані, обернено пропорційній силам. |
Коли на тіло діють декілька паралельних сил, то їх рівнодійну можна знайти послідовно, використовуючи правила складання двох паралельних сил.
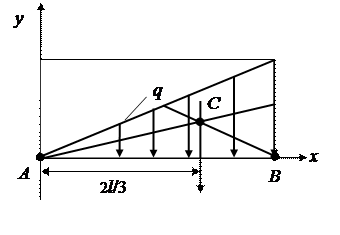
У випадку розподілених сил діють наступним способом. Силу ваги тіла показують у вигляді рівнодійної, яка має початок у центрі С ваги і спрямована завжди вертикально донизу (рис. 4.8,а). Якщо сили розподілені за довжиною, то діють так: у випадку прямокутної епюри (рис. 4.8,б) сили замінюють рівнодійною  (l – довжина відрізка АВ прикладання сил), яка прикладена у середині відрізка АВ; при лінійному законі розподілу сили (рис. 4.8,в) рівнодійна
(l – довжина відрізка АВ прикладання сил), яка прикладена у середині відрізка АВ; при лінійному законі розподілу сили (рис. 4.8,в) рівнодійна 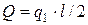 прикладена у точці з координатою
прикладена у точці з координатою  ; при довільному законі (рис. 4.8,г) – величину рівнодійної сили визначають формулою
; при довільному законі (рис. 4.8,г) – величину рівнодійної сили визначають формулою  , а координату її прикладання -
, а координату її прикладання - 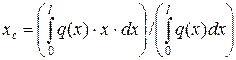 . Однак завжди лінія дії рівнодійної проходить через центр ваги площи епюри розподілених сил (наприклад, у випадку лінійного закону розподілу сил (рис. 4.8,в) вона проходить через точку перетину медіан трикутника).
. Однак завжди лінія дії рівнодійної проходить через центр ваги площи епюри розподілених сил (наприклад, у випадку лінійного закону розподілу сил (рис. 4.8,в) вона проходить через точку перетину медіан трикутника).
а |
б | |||||||||||||||
в |
г |
Рис. 4.8

 і
і 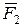 , причому нехай за величиною
, причому нехай за величиною  (рис. 4.7). Візьмемо на продовженні відрізка ВА точку С і прикладемо в ній двійку сил
(рис. 4.7). Візьмемо на продовженні відрізка ВА точку С і прикладемо в ній двійку сил  і
і  , які паралельні силам
, які паралельні силам  (4.6)
(4.6) , тобто дорівнює за величиною силі
, тобто дорівнює за величиною силі  , як зрівноважені, можна відкинути (закреслено на рис. 4.7). У результаті задані сили
, як зрівноважені, можна відкинути (закреслено на рис. 4.7). У результаті задані сили 

 Q
Q
 F 2
F 2


 B A C
B A C








