Парою сил називається система двох, розташованих в одній площині паралельних сил  , які рівні за величиною і протилежно направлені.
, які рівні за величиною і протилежно направлені.
Площина S, яка проходить через лінії дії сил пари (рис. 4.8), називається площиною дії пари.
що вектор  (
( ) моменту пари сил напрямлений перпендикулярно до площини S дії пари сил у той бік, звідки обертання пари відбувається проти ходу стрілки годинника.
) моменту пари сил напрямлений перпендикулярно до площини S дії пари сил у той бік, звідки обертання пари відбувається проти ходу стрілки годинника.
Відповідно до механічної схеми на рис. 4.8 отримаємо наступні властивості моменту пари сил:
- за величиною момент пари сил дорівнюватиме модулю вектора  (
( ):
):
 (
( )
) 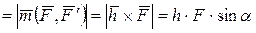 .
.
Звичайно при побудові схеми на рис. 4.8 приймають кут  , тоді матимемо
, тоді матимемо 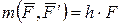 . У цьому випадку h визначають плечем пари сил (найкоротший відрізок між лініями дії сил, що складають пару);
. У цьому випадку h визначають плечем пари сил (найкоротший відрізок між лініями дії сил, що складають пару);
- пара сил не має рівнодійної, тому що при  виконується рівність
виконується рівність  ; при цьому властивості сумісної механічної (обертальної) дії сил пари на тіло зберігаються і проявляються у вигляді моменту
; при цьому властивості сумісної механічної (обертальної) дії сил пари на тіло зберігаються і проявляються у вигляді моменту  пари, рівному сумі моментів
пари, рівному сумі моментів  заданих сил відносно будь-якої точки О тіла. Нехай, наприклад, точка О на рис. 4.8 – довільна точка простору, а
заданих сил відносно будь-якої точки О тіла. Нехай, наприклад, точка О на рис. 4.8 – довільна точка простору, а  радіуси-вектори точок прикладання сил
радіуси-вектори точок прикладання сил 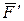 і
і  пари. З визначення моменту сили відносно точки маємо
пари. З визначення моменту сили відносно точки маємо
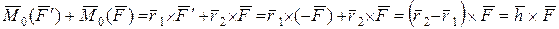
або  . (4.7)
. (4.7)
З виразу (4.7) виходить, що момент прикладеної до тіла пари сил ( ) дорівнює сумі моментів цих сил відносно точки О і не залежить від її положення у просторі.
) дорівнює сумі моментів цих сил відносно точки О і не залежить від її положення у просторі.
Інші властивості пари сил визначаються наступними теоремами.
Теорема про еквівалентність пар. Не змінюючи дії на тіло, пару сил можна замінити іншою парою, яка лежить в цій самій площині і має такий самий момент за величиною і напрямом.
Доведення. Нехай на тіло діє пара сил  з плечем d1 ( рис. 4.9). Проведемо у площині дії пари сил через довільні точки D і С двіпаралельні прямі до перетину їх з лініями дій сил пари в точках А і В. Відстані між прямими АС і BD позначимо як d 2. Розкладемо сили
з плечем d1 ( рис. 4.9). Проведемо у площині дії пари сил через довільні точки D і С двіпаралельні прямі до перетину їх з лініями дій сил пари в точках А і В. Відстані між прямими АС і BD позначимо як d 2. Розкладемо сили  і
і 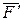 за напрямами AB,
за напрямами AB,
BD i AC. За побудовою очевидно, що  , тоді сили , тоді сили  і і  , як зрівноважені, можна відкинути. Сили , як зрівноважені, можна відкинути. Сили  і і  перенесемо уздовж їх ліній дій у точки D і С. У результаті проведених перетворень задану пару сил перенесемо уздовж їх ліній дій у точки D і С. У результаті проведених перетворень задану пару сил  було замінено новою парою було замінено новою парою  з іншим плечем з іншим плечем  та іншими силами. Через довільність вибору точок D, С і напрямів прямих BD і AС нова пара сил та іншими силами. Через довільність вибору точок D, С і напрямів прямих BD і AС нова пара сил
|   Рис. 4.9
Рис. 4.9
|
може бути розташована у площині її дії де завгодно.
Покажемо, що моменти нової і заданої пар сил  i
i  рівні. За побудовою сила
рівні. За побудовою сила  , а сила
, а сила  проходить через точку А, тому буде виконуватись:
проходить через точку А, тому буде виконуватись:
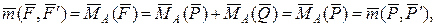
тобто  (4.8)
(4.8)
З рівностей (4.8) випливають такі додаткові властивості пар сил:
- задану пару сил, не змінюючи її дії на тіло, можна переносити як завгодно у площині її дії;
- у заданої пари сил можна змінювати сили і довжину плеча, щоб залишався незмінним її момент;
- дві пари, що лежать в одній площині і мають однакові моменти, є еквівалентними;
- момент пари сил є вільним вектором: його можна переносити паралельно самому собі в будь-яку точку тіла.
Теорема про перенесення пари в паралельну площину. Дія пари сил на тіло не порушиться, якщо її перенести із заданої площини у довільну іншу площину, яка паралельна заданій.
де прикладена в точці С – середині відрізка AE. Аналогічно сили 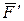 і
і 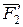 зводяться до рівнодійної
зводяться до рівнодійної 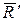 , прикладеної в середині відрізка ВD, тобто в точці С. За побудовою і визначенням рівнодійні сили
, прикладеної в середині відрізка ВD, тобто в точці С. За побудовою і визначенням рівнодійні сили  і
і 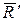 будуть рівними і протилежно направленими, тому їх можна відкинути. У результаті задана пара сил
будуть рівними і протилежно направленими, тому їх можна відкинути. У результаті задана пара сил  перетворюється в пару сил
перетворюється в пару сил  , яка розміщена у площині
, яка розміщена у площині  .
.
З доведеної теореми випливає, що дві пари, які лежать в одній площині або в паралельних площинах і мають однакові моменти, еквівалентні.
Теорема про додавання пар сил. Довільну систему двох пар сил можна замінити рівнодійною парою. Момент рівнодійної пари дорівнює векторній сумі моментів початкових пар.
 Доведення. Розглянемо пари сил з моментами
Доведення. Розглянемо пари сил з моментами  і
і  , які лежать у довільних площинах
, які лежать у довільних площинах  і
і  , що перетинаються (рис. 4.11). Визначимо на лінії перетину цих площин відрізок АВ =d і позначимо його вектором
, що перетинаються (рис. 4.11). Визначимо на лінії перетину цих площин відрізок АВ =d і позначимо його вектором  .
.
Визначимо пару сил з моментом  силами ( силами ( ), а пару сил з моментом ), а пару сил з моментом  - силами ( - силами (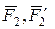 ), прикладеними в точках А і В. При цьому виконуватиметься ), прикладеними в точках А і В. При цьому виконуватиметься  = F 1 d, = F 1 d,  = F 2 d. Додаючи прикладені в точках A і В сили, замінимо системи сил = F 2 d. Додаючи прикладені в точках A і В сили, замінимо системи сил  i i  силами силами  , ,
|  Рис. 4.11
Рис. 4.11
|
які за визначенням складуть пару сил  . Момент рівнодійної пари
. Момент рівнодійної пари  , оскільки
, оскільки  , визначатиметься як
, визначатиметься як
 (4.9)
(4.9)
Якщо на тіло діє п пар сил з моментами 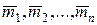 ,то, застосовуючи послідовно формулу (4.9), одержимо (рис. 4.12), що задана система пар сил зводиться до результуючої пари з моментом
,то, застосовуючи послідовно формулу (4.9), одержимо (рис. 4.12), що задана система пар сил зводиться до результуючої пари з моментом
 (4.10)
(4.10)
Тут результуючу пару  визначають (див. силовий многокутник у розділі 3) замикаючою стороною многокутника векторів
визначають (див. силовий многокутник у розділі 3) замикаючою стороною многокутника векторів  .
.
Якщо пари сил лежать в одній площині, то вектори їх моментів будуть паралельні. Тому момент результуючої пари  дорівнює алгебраїчній сумі складових моментів:
дорівнює алгебраїчній сумі складових моментів:
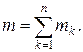
 Рис. 4.12
Рис. 4.12
| Момент результуючої пари сил  можна визначити аналітично, спроектувавши векторне рівняння (4.10) на осі системи координат: можна визначити аналітично, спроектувавши векторне рівняння (4.10) на осі системи координат:



|
Величину (модуль вектора  ) результуючої пари визначають як
) результуючої пари визначають як
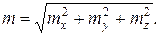


 При побудові вектора
При побудові вектора  у просторі, тобто при визначенні площини дії результуючої пари сил звичайно використовують його напрямні косинуси:
у просторі, тобто при визначенні площини дії результуючої пари сил звичайно використовують його напрямні косинуси:
 ,
, 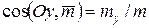 ,
,  .
.

 , які рівні за величиною і протилежно направлені.
, які рівні за величиною і протилежно направлені. ) математично визначається вектором
) математично визначається вектором  (
( . Отже, враховуючи його властивості, отримаємо,
. Отже, враховуючи його властивості, отримаємо,



 (
(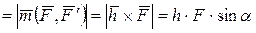 .
. , тоді матимемо
, тоді матимемо 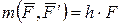 . У цьому випадку h визначають плечем пари сил (найкоротший відрізок між лініями дії сил, що складають пару);
. У цьому випадку h визначають плечем пари сил (найкоротший відрізок між лініями дії сил, що складають пару); виконується рівність
виконується рівність  ; при цьому властивості сумісної механічної (обертальної) дії сил пари на тіло зберігаються і проявляються у вигляді моменту
; при цьому властивості сумісної механічної (обертальної) дії сил пари на тіло зберігаються і проявляються у вигляді моменту  пари, рівному сумі моментів
пари, рівному сумі моментів  заданих сил відносно будь-якої точки О тіла. Нехай, наприклад, точка О на рис. 4.8 – довільна точка простору, а
заданих сил відносно будь-якої точки О тіла. Нехай, наприклад, точка О на рис. 4.8 – довільна точка простору, а  радіуси-вектори точок прикладання сил
радіуси-вектори точок прикладання сил 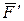 і
і  пари. З визначення моменту сили відносно точки маємо
пари. З визначення моменту сили відносно точки маємо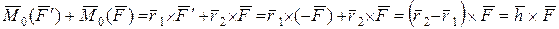
 . (4.7)
. (4.7) ) дорівнює сумі моментів цих сил відносно точки О і не залежить від її положення у просторі.
) дорівнює сумі моментів цих сил відносно точки О і не залежить від її положення у просторі. з плечем d1 ( рис. 4.9). Проведемо у площині дії пари сил через довільні точки D і С двіпаралельні прямі до перетину їх з лініями дій сил пари в точках А і В. Відстані між прямими АС і BD позначимо як d 2. Розкладемо сили
з плечем d1 ( рис. 4.9). Проведемо у площині дії пари сил через довільні точки D і С двіпаралельні прямі до перетину їх з лініями дій сил пари в точках А і В. Відстані між прямими АС і BD позначимо як d 2. Розкладемо сили 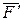 за напрямами AB,
за напрямами AB, , тоді сили
, тоді сили  і
і  , як зрівноважені, можна відкинути. Сили
, як зрівноважені, можна відкинути. Сили  і
і  перенесемо уздовж їх ліній дій у точки D і С. У результаті проведених перетворень задану пару сил
перенесемо уздовж їх ліній дій у точки D і С. У результаті проведених перетворень задану пару сил  з іншим плечем
з іншим плечем  та іншими силами. Через довільність вибору точок D, С і напрямів прямих BD і AС нова пара сил
та іншими силами. Через довільність вибору точок D, С і напрямів прямих BD і AС нова пара сил

 Рис. 4.9
Рис. 4.9
 , а сила
, а сила 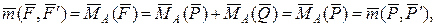
 (4.8)
(4.8)





 За побудовою фігура ABЕД єпаралелограмом. Далі додамо пара-лельні сили
За побудовою фігура ABЕД єпаралелограмом. Далі додамо пара-лельні сили  . Їх рівнодійна
. Їх рівнодійна  бу-
бу-
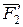 зводяться до рівнодійної
зводяться до рівнодійної 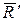 , прикладеної в середині відрізка ВD, тобто в точці С. За побудовою і визначенням рівнодійні сили
, прикладеної в середині відрізка ВD, тобто в точці С. За побудовою і визначенням рівнодійні сили  , яка розміщена у площині
, яка розміщена у площині  .
. Доведення. Розглянемо пари сил з моментами
Доведення. Розглянемо пари сил з моментами  і
і  , які лежать у довільних площинах
, які лежать у довільних площинах  і
і  .
. ), а пару сил з моментом
), а пару сил з моментом 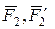 ), прикладеними в точках А і В. При цьому виконуватиметься
), прикладеними в точках А і В. При цьому виконуватиметься  = F 1 d,
= F 1 d,  = F 2 d. Додаючи прикладені в точках A і В сили, замінимо системи сил
= F 2 d. Додаючи прикладені в точках A і В сили, замінимо системи сил  силами
силами  ,
,
 Рис. 4.11
Рис. 4.11
 . Момент рівнодійної пари
. Момент рівнодійної пари  , визначатиметься як
, визначатиметься як (4.9)
(4.9)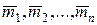 ,то, застосовуючи послідовно формулу (4.9), одержимо (рис. 4.12), що задана система пар сил зводиться до результуючої пари з моментом
,то, застосовуючи послідовно формулу (4.9), одержимо (рис. 4.12), що задана система пар сил зводиться до результуючої пари з моментом (4.10)
(4.10) визначають (див. силовий многокутник у розділі 3) замикаючою стороною многокутника векторів
визначають (див. силовий многокутник у розділі 3) замикаючою стороною многокутника векторів  .
. 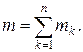
 Рис. 4.12
Рис. 4.12



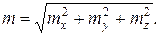

 При побудові вектора
При побудові вектора  ,
, 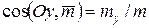 ,
,  .
.


