Властивості головного вектора, головного момента і результуючої приєднаної пари системи сил. Статичні інваріанти
Величини і напрямки головних векторів
де
х Рис. 5.4
Кут
Якщо на практиці при вирішенні задач рівноваги твердого тіла виникає питання зміни центра приведення системи сил з точки О у наперед задану точку О 1, то головний вектор, головний момент і момент результуючої приєднаної пари системи сил мають наступні властивості. Враховуючи вирази (5.2), (5.8) є очевидним, що головний вектор системи сил ні за величиною, ні за напрямком не залежить від положення центра приведення, тобто завжди виконуватиметься рівність У механіці головний вектор
де п - номер поточної точки приведення. Момент результуючої приєднаної пари вихідної системи сил при перенесенні центра приведення буде визначатися (рис. 5.5) за формулою
де На рис. 5.5 вектор
Рис. 5.5
Вираз (5.9) отримано за допомогою наступних еквівалентних системних перетворень:
де При цьому використано лему про паралельне перенесення сили
З рівняння (5.10) виходить, що момент Головний момент системи сил при перенесенні центра приведення вихідної системи сил матиме, в свою чергу, наступну властивість. Враховуючи вираз (5.3) і рис. 5.6, отримаємо:
Аk
Рис. 5.6
З рівняння (5.11) випливає, що головний момент вихідної системи сил при перенесенні центра приведення до точки О 1 змінюється на величину моменту Враховуючи рівняння (5.5) і (5.7) отримаємо вирази:
Рис. 5.7 Однак, на практиці виявилось, що більш зручним у використанні є рівняння (5.11), яке стосується головного моменту системи сил. Розглянемо далі інші властивості головного вектора Важливою властивістю головних вектора Дійсно, для будь-якої точки приведення О 1 отримаємо:
За визначенням вектор
Вираз (5.14), в результаті незалежності головного вектора системи сил від зміни полюса приведення, перетворюється у рівність
яка і доводить зазначену властивість. У механіці цю властивість скалярного добутку головного вектора і головного моменту системи сил визначають як другий статичний інваріант (перша форма). Розглянемо другу форму другого статичного інваріанта системи діючих на тіло сил, які зведено в центрі О до головного вектора
де Тоді з формул (5.15), (5.16) випливає вираз
який, з урахуванням рівності
Співвідношення (5.17) виявляє, що проекція головного моменту систем сил на напрямок її головного вектора не залежить від положення точки приведення. У механіці цю властивість визначають як другий статичний інваріант (друга форма).
|

 і
і  у системі координат Oxyz (рис. 5.4) визначаються за правилами векторної алгебри формулами
у системі координат Oxyz (рис. 5.4) визначаються за правилами векторної алгебри формулами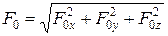 ;
;  , (5.8)
, (5.8) ;
; 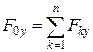 ;
;  ;
;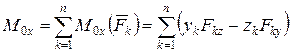 ;
; 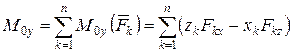 ;
;

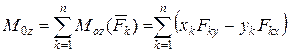 ;
;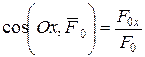 ;
; 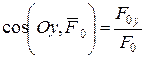 ;
;  ;
; ;
; 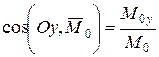 ;
;  .
.
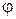 між векторами
між векторами  .
.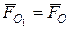 (точка О 1 - новий центр приведення). Це обумовлено тим, що за формулою визначення (
(точка О 1 - новий центр приведення). Це обумовлено тим, що за формулою визначення ( ) головний вектор є функцією тільки параметрів сил початкової системи і не залежить від положення точки О на тілі.
) головний вектор є функцією тільки параметрів сил початкової системи і не залежить від положення точки О на тілі. називається першим статичним інваріантом. Це означає, що для будь-якої вихідної системи сил його величина і напрямок є сталими величинами, тобто незалежними (інваріантними) до вибору центра приведення:
називається першим статичним інваріантом. Це означає, що для будь-якої вихідної системи сил його величина і напрямок є сталими величинами, тобто незалежними (інваріантними) до вибору центра приведення: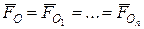 ,
, , (5.9)
, (5.9) - момент приєднаної пари сил.
- момент приєднаної пари сил.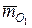 є, за правилом векторного добутку, перпендикулярним що площини Е, якій належать вектори
є, за правилом векторного добутку, перпендикулярним що площини Е, якій належать вектори 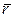 і
і  , тобто
, тобто 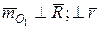 .
.
 ,
,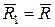 .
. , рівним моменту
, рівним моменту  вихідної сили
вихідної сили  (моменту приєднаної пари сил у точці О) як вільного вектора, який можна переносити паралельно самому собі в будь-яку точку тіла (в даному випадку з точки О у точці О 1). Крім того, використано властивості геометричного додавання векторів моментів пар сил у точці О 1, тобто:
(моменту приєднаної пари сил у точці О) як вільного вектора, який можна переносити паралельно самому собі в будь-яку точку тіла (в даному випадку з точки О у точці О 1). Крім того, використано властивості геометричного додавання векторів моментів пар сил у точці О 1, тобто:

 . (5.11)
. (5.11)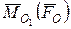 головного вектора
головного вектора 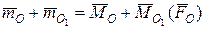 ,
,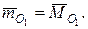 (5.12)
(5.12) З виразу (5.12) випливає рівність моментів результуючої пари і головного моменту системи сил відносно нового центра зведення О 1, а також справедливість приведених на рис. 5.7 системних перетворень.
З виразу (5.12) випливає рівність моментів результуючої пари і головного моменту системи сил відносно нового центра зведення О 1, а також справедливість приведених на рис. 5.7 системних перетворень. системи сил, які мають суттєве теоретичне і практичне значення.
системи сил, які мають суттєве теоретичне і практичне значення.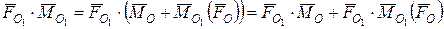 . (5.13)
. (5.13)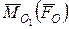 і вектор
і вектор 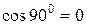 , до виду
, до виду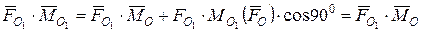 . (5.14)
. (5.14) , (5.15)
, (5.15) З векторної алгебри відомо, що за величиною скалярний добуток двох векторів може бути визначеним через проекцію одного з векторів добутку на напрямок іншого:
З векторної алгебри відомо, що за величиною скалярний добуток двох векторів може бути визначеним через проекцію одного з векторів добутку на напрямок іншого:
 , (5.16)
, (5.16)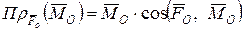 - проекція вектора
- проекція вектора  ,
, першого статичного інваріанта, перетворюється до вигляду
першого статичного інваріанта, перетворюється до вигляду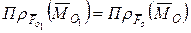 . (5.17)
. (5.17)


