центра. Теорема Пуансо (Основна теорема статики)
Розглядаючи системи збіжних і паралельних сил у просторі, ми переконалися, що вони приводяться лише до одного силового фактора: рівнодійної сили або до пари сил.
Розглянемо тепер задачу приведення довільної систем сил  у просторі до заданого центра О (теорема належить Пуансо, 1777 - 1859 рр.).
у просторі до заданого центра О (теорема належить Пуансо, 1777 - 1859 рр.).
Теорема: Довільна система сил  у просторі зводиться до заданого центра О сукупністю двох силових факторів: сили
у просторі зводиться до заданого центра О сукупністю двох силових факторів: сили  , рівній головному вектору
, рівній головному вектору  вихідної системи сил і прикладеній у центрі приведення О, і пари сил, момент
вихідної системи сил і прикладеній у центрі приведення О, і пари сил, момент  якої дорівнює головному моменту
якої дорівнює головному моменту  системи сил відносно того ж центра.
системи сил відносно того ж центра.
Доведення. Розглянемо вихідну довільну систему сил  у просторі (рис. 5.3,а). Нехай сили є прикладеними до тіла в точках
у просторі (рис. 5.3,а). Нехай сили є прикладеними до тіла в точках  , координати яких визначено радіусами-векторами
, координати яких визначено радіусами-векторами  у системі координат Оxyz, полюс якої співпадає з центром приведення О.
у системі координат Оxyz, полюс якої співпадає з центром приведення О.
Введемо такі позначення і поняття.
Головний вектор системи сил 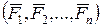 - вектор
- вектор  , який дорівнює геометричній сумі прикладених до тіла сил системи:
, який дорівнює геометричній сумі прикладених до тіла сил системи:
 , (5.2)
, (5.2)
де індекс О визначає точку прикладання вектора  до тіла.
до тіла.
а б

в г
Рис. 5.3
Головний момент системи сил відносно точки О - вектор  , що дорівнює геометричній сумі моментів сил вихідної системи відносно тієї ж точки:
, що дорівнює геометричній сумі моментів сил вихідної системи відносно тієї ж точки:
 . (5.3)
. (5.3)
Таким чином, за визначенням вектори  і
і  відносяться, з точки зору векторної алгебри, до зв’язаних у точці О векторів.
відносяться, з точки зору векторної алгебри, до зв’язаних у точці О векторів.
Для кожної з сил системи використуємо лему про паралельне перенесення сили у полюс О. У результаті перетворень отримаємо систему збіжних у точці О (рис. 5.3,б) сил  , що, як нам відомо, еквівалентна одній силі
, що, як нам відомо, еквівалентна одній силі  (рівнодійній), що дорівнює їх геометричній сумі:
(рівнодійній), що дорівнює їх геометричній сумі:
 . (5.4)
. (5.4)
Між векторами  збіжної і
збіжної і  вихідної систем сил існують співвідношення:
вихідної систем сил існують співвідношення:  ). Якщо розглянути геометричну суму векторів
). Якщо розглянути геометричну суму векторів  сил вихідної системи у точці О як вектор математичний і позначити його, відповідно до (5.2), як головний вектор
сил вихідної системи у точці О як вектор математичний і позначити його, відповідно до (5.2), як головний вектор  вихідної системи сил, то отримаємо наступну рівність
вихідної системи сил, то отримаємо наступну рівність
 . (5.5)
. (5.5)
З рівнянь (5.2), (5.4) і (5.5) виходить, таким чином, що сила  за математичним змістом дорівнює головному вектору
за математичним змістом дорівнює головному вектору  вихідної системи. У свою чергу, на відміну від сили
вихідної системи. У свою чергу, на відміну від сили  , головний вектор
, головний вектор  не має, стосовно розглядуваного тіла фізичного змісту, тому що точки
не має, стосовно розглядуваного тіла фізичного змісту, тому що точки 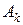 прикладання складаючих сил
прикладання складаючих сил  (рис. 5.3,а) не співпадають з центром приведення О, в якому прикладений головний вектор.
(рис. 5.3,а) не співпадають з центром приведення О, в якому прикладений головний вектор.
При паралельному перенесенні сили  до тіла необхідно приєднати одночасно пару сил
до тіла необхідно приєднати одночасно пару сил  з моментом
з моментом  , прикладеним (рис. 5.3,в) у точці О. Система приєднаних пар
, прикладеним (рис. 5.3,в) у точці О. Система приєднаних пар  , відповідно до теореми про додавання пар сил, зводиться до результуючої пари з моментом
, відповідно до теореми про додавання пар сил, зводиться до результуючої пари з моментом
 (5.6)
(5.6)
у точці О.
Відповідно до (5.3) і (5.6) отримаємо, що момент  приєднаної
приєднаної
пари дорівнює головному моменту 
 вихідної системи сил відносно центра приведення О, тобто (рис. 5.3,в)
вихідної системи сил відносно центра приведення О, тобто (рис. 5.3,в)
 . (5.7)
. (5.7)
Отже (рис. 5.3,г) вихідну систему сил  зведено в довільно обраній точці О до еквівалентної системи
зведено в довільно обраній точці О до еквівалентної системи  двох силових факторів: сили
двох силових факторів: сили  , яка дорівнює головному вектору
, яка дорівнює головному вектору  цієї системи сил, і пари сил з моментом
цієї системи сил, і пари сил з моментом  , який дорівнює головному моменту
, який дорівнює головному моменту  системи сил відносно центра приведення.
системи сил відносно центра приведення.
Таким чином, теорему доведено. Ця теорема має назву основної теореми статики (теорема Пуансо).
З доведеної вище теореми випливає, що дві системи сил  і
і  будуть статично еквівалентними, якщо їх головні вектори й головні моменти у довільно обраному центрі приведення рівні між собою. Отже, для характеристики системи діючих на тіло сил є абсолютно достатнім визначити у довільному центрі О головний вектор
будуть статично еквівалентними, якщо їх головні вектори й головні моменти у довільно обраному центрі приведення рівні між собою. Отже, для характеристики системи діючих на тіло сил є абсолютно достатнім визначити у довільному центрі О головний вектор  і головний момент
і головний момент  вихідної системи сил і задати їх на розрахунковій схемі (рис. 5.3,г). При цьому будемо враховувати, по-перше, те, що точки приведення сили
вихідної системи сил і задати їх на розрахунковій схемі (рис. 5.3,г). При цьому будемо враховувати, по-перше, те, що точки приведення сили  і моменту
і моменту  , а також точки прикладання головних векторів
, а також точки прикладання головних векторів  і
і  співпадають за визначенням, а по-другому, що вектор
співпадають за визначенням, а по-другому, що вектор  і вектор
і вектор  , на відміну від зв’язаних у точці О векторів
, на відміну від зв’язаних у точці О векторів  і
і  , є відповідно ковзним і вільним векторами.
, є відповідно ковзним і вільним векторами.

 у просторі до заданого центра О (теорема належить Пуансо, 1777 - 1859 рр.).
у просторі до заданого центра О (теорема належить Пуансо, 1777 - 1859 рр.). , рівній головному вектору
, рівній головному вектору  вихідної системи сил і прикладеній у центрі приведення О, і пари сил, момент
вихідної системи сил і прикладеній у центрі приведення О, і пари сил, момент  якої дорівнює головному моменту
якої дорівнює головному моменту  системи сил відносно того ж центра.
системи сил відносно того ж центра. , координати яких визначено радіусами-векторами
, координати яких визначено радіусами-векторами  у системі координат Оxyz, полюс якої співпадає з центром приведення О.
у системі координат Оxyz, полюс якої співпадає з центром приведення О.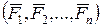 - вектор
- вектор  , (5.2)
, (5.2)


 . (5.3)
. (5.3) , що, як нам відомо, еквівалентна одній силі
, що, як нам відомо, еквівалентна одній силі  . (5.4)
. (5.4) збіжної і
збіжної і  вихідної систем сил існують співвідношення:
вихідної систем сил існують співвідношення:  ). Якщо розглянути геометричну суму векторів
). Якщо розглянути геометричну суму векторів  сил вихідної системи у точці О як вектор математичний і позначити його, відповідно до (5.2), як головний вектор
сил вихідної системи у точці О як вектор математичний і позначити його, відповідно до (5.2), як головний вектор  . (5.5)
. (5.5)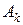 прикладання складаючих сил
прикладання складаючих сил  з моментом
з моментом  , прикладеним (рис. 5.3,в) у точці О. Система приєднаних пар
, прикладеним (рис. 5.3,в) у точці О. Система приєднаних пар  , відповідно до теореми про додавання пар сил, зводиться до результуючої пари з моментом
, відповідно до теореми про додавання пар сил, зводиться до результуючої пари з моментом (5.6)
(5.6) приєднаної
приєднаної
 вихідної системи сил відносно центра приведення О, тобто (рис. 5.3,в)
вихідної системи сил відносно центра приведення О, тобто (рис. 5.3,в) . (5.7)
. (5.7) зведено в довільно обраній точці О до еквівалентної системи
зведено в довільно обраній точці О до еквівалентної системи  двох силових факторів: сили
двох силових факторів: сили  будуть статично еквівалентними, якщо їх головні вектори й головні моменти у довільно обраному центрі приведення рівні між собою. Отже, для характеристики системи діючих на тіло сил є абсолютно достатнім визначити у довільному центрі О головний вектор
будуть статично еквівалентними, якщо їх головні вектори й головні моменти у довільно обраному центрі приведення рівні між собою. Отже, для характеристики системи діючих на тіло сил є абсолютно достатнім визначити у довільному центрі О головний вектор 


