Особливістю розглядуваної системи сил  є приналежність ліній дій всіх сил системи площині Е (рис. 5.19,а). У цьому випадку вихідну систему сил, використовуючи теорему Пуансо, в центрі приведення О (рис. 5.19,б) можна звести взагалі до двох силових факторів: сили
є приналежність ліній дій всіх сил системи площині Е (рис. 5.19,а). У цьому випадку вихідну систему сил, використовуючи теорему Пуансо, в центрі приведення О (рис. 5.19,б) можна звести взагалі до двох силових факторів: сили  , яка дорівнює головному вектору
, яка дорівнює головному вектору  , і результуючої приєднаної пари сил
, і результуючої приєднаної пари сил  з моментом
з моментом  (показано також дуговою стрілкою на рис. 5.19,б), рівним головному моменту
(показано також дуговою стрілкою на рис. 5.19,б), рівним головному моменту  вихідної системи сил.
вихідної системи сил.

а
б
Рис. 5.19

 На відміну від довільної системи сил у просторі тут: головний вектор
На відміну від довільної системи сил у просторі тут: головний вектор  довільної плоскої системи сил завжди належить площині Е, яка є площиною дії пари
довільної плоскої системи сил завжди належить площині Е, яка є площиною дії пари  ; головний момент
; головний момент  , тобто кут
, тобто кут 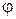 між векторами дорівнюватиме
між векторами дорівнюватиме  .
.
Відповідно до зображених на рис. 5.19,б силових факторів матимуть місце, залежно від величин головних векторів  ,
,  зведеної у центрі О системи сил, такі випадки приведення довільної системи сил у площині.
зведеної у центрі О системи сил, такі випадки приведення довільної системи сил у площині.
5.5.1. Приведення до пари сил  , коли головний вектор системи
, коли головний вектор системи  =0, а головний момент
=0, а головний момент  . Цей випадок за сукупністю діючих на тіло силових факторів повністю співпадає з випадком приведення довільної системи сил у просторі, розглянутомум у п. 5.4.1 і на рис. 5.8. Наприклад, для зображених на рис. 5.20,а системи двох сил
. Цей випадок за сукупністю діючих на тіло силових факторів повністю співпадає з випадком приведення довільної системи сил у просторі, розглянутомум у п. 5.4.1 і на рис. 5.8. Наприклад, для зображених на рис. 5.20,а системи двох сил 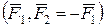 отримаємо для центру приведення О (рис. 5.20,б):
отримаємо для центру приведення О (рис. 5.20,б):  ;
;  ;
;  пл. Е; система сил
пл. Е; система сил  .
.

а б
Рис. 5.20
5.5.2. Приведення до рівнодійної  у центрі О. Тут головний момент системи
у центрі О. Тут головний момент системи  =0, головний вектор
=0, головний вектор  , а вихідна система сил зводиться тільки до однієї сили
, а вихідна система сил зводиться тільки до однієї сили  , що є рівнодійною
, що є рівнодійною  , прикладеною у точці О. Випадок ідентичний розглянутому у п. 5.4.2 і на рис. 5.9.
, прикладеною у точці О. Випадок ідентичний розглянутому у п. 5.4.2 і на рис. 5.9.
 Приклад приведення:
Приклад приведення:  (рис. 5.21,а),
(рис. 5.21,а),  . У точці О буде:
. У точці О буде:  ;
;  (рис. 5.21,б); рівнодійна сила
(рис. 5.21,б); рівнодійна сила  прикладена у центрі приведення О; системи сил
прикладена у центрі приведення О; системи сил  .
.

а б
Рис. 5.21
5.5.3. Зрівноважена система сил: у центрі приведення О маємо  =0 і
=0 і  =0. При цьому (див. п. 5.4.3 і рис. 5.10, 5.11) многокутники діючих на тіло сил
=0. При цьому (див. п. 5.4.3 і рис. 5.10, 5.11) многокутники діючих на тіло сил  і моментів приєднаних пар сил
і моментів приєднаних пар сил  є замкненими і вихідна система сил еквівалентна нулю
є замкненими і вихідна система сил еквівалентна нулю  , тобто є зрівноваженою. Тут, наприклад, для системи двох сил:
, тобто є зрівноваженою. Тут, наприклад, для системи двох сил:  і
і 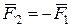 (рис. 5.22,а), буде:
(рис. 5.22,а), буде:  ;
;  (рис. 5.22,б); система сил
(рис. 5.22,б); система сил  .
.

а б
Рис. 5.22
 5.5.4. У загальному випадку, зведену в центрі О до головного вектора
5.5.4. У загальному випадку, зведену в центрі О до головного вектора  і головного моменту
і головного моменту  вихідну систему сил можна подальшими спрощеннями звести до однієї сили, рівнодійної
вихідну систему сил можна подальшими спрощеннями звести до однієї сили, рівнодійної  , яка прикладена, на відміну від п. 5.5.2 у новому центрі О 1 на відстані
, яка прикладена, на відміну від п. 5.5.2 у новому центрі О 1 на відстані  від точки О. Цей випадок повністю співпадає за доведенням з випадком приведення, який розглянуто стосовно довільної системи сил у просторі у п. 5.4.4.3 і на рис. 5.18. Наприклад, для зображеної на рис. 5.23,а системи трьох сил: (
від точки О. Цей випадок повністю співпадає за доведенням з випадком приведення, який розглянуто стосовно довільної системи сил у просторі у п. 5.4.4.3 і на рис. 5.18. Наприклад, для зображеної на рис. 5.23,а системи трьох сил: ( ,
, 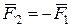 ,
,  ) отримаємо у центрах приведення О, О 1:
) отримаємо у центрах приведення О, О 1:  (рис. 5.23,б);
(рис. 5.23,б);  ;
;  ;
;  (рис. 5.23,в), система сил
(рис. 5.23,в), система сил  .
.
а
б в
Рис. 5.23

 є приналежність ліній дій всіх сил системи площині Е (рис. 5.19,а). У цьому випадку вихідну систему сил, використовуючи теорему Пуансо, в центрі приведення О (рис. 5.19,б) можна звести взагалі до двох силових факторів: сили
є приналежність ліній дій всіх сил системи площині Е (рис. 5.19,а). У цьому випадку вихідну систему сил, використовуючи теорему Пуансо, в центрі приведення О (рис. 5.19,б) можна звести взагалі до двох силових факторів: сили  , яка дорівнює головному вектору
, яка дорівнює головному вектору  , і результуючої приєднаної пари сил
, і результуючої приєднаної пари сил  з моментом
з моментом  (показано також дуговою стрілкою на рис. 5.19,б), рівним головному моменту
(показано також дуговою стрілкою на рис. 5.19,б), рівним головному моменту  вихідної системи сил.
вихідної системи сил.

 На відміну від довільної системи сил у просторі тут: головний вектор
На відміну від довільної системи сил у просторі тут: головний вектор  довільної плоскої системи сил завжди належить площині Е, яка є площиною дії пари
довільної плоскої системи сил завжди належить площині Е, яка є площиною дії пари  , тобто кут
, тобто кут 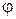 між векторами дорівнюватиме
між векторами дорівнюватиме  .
. . Цей випадок за сукупністю діючих на тіло силових факторів повністю співпадає з випадком приведення довільної системи сил у просторі, розглянутомум у п. 5.4.1 і на рис. 5.8. Наприклад, для зображених на рис. 5.20,а системи двох сил
. Цей випадок за сукупністю діючих на тіло силових факторів повністю співпадає з випадком приведення довільної системи сил у просторі, розглянутомум у п. 5.4.1 і на рис. 5.8. Наприклад, для зображених на рис. 5.20,а системи двох сил 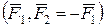 отримаємо для центру приведення О (рис. 5.20,б):
отримаємо для центру приведення О (рис. 5.20,б):  ;
;  ;
;  пл. Е; система сил
пл. Е; система сил  .
.
 , а вихідна система сил зводиться тільки до однієї сили
, а вихідна система сил зводиться тільки до однієї сили  Приклад приведення:
Приклад приведення:  (рис. 5.21,а),
(рис. 5.21,а),  . У точці О буде:
. У точці О буде:  ;
;  (рис. 5.21,б); рівнодійна сила
(рис. 5.21,б); рівнодійна сила  прикладена у центрі приведення О; системи сил
прикладена у центрі приведення О; системи сил  .
.
 і моментів приєднаних пар сил
і моментів приєднаних пар сил  є замкненими і вихідна система сил еквівалентна нулю
є замкненими і вихідна система сил еквівалентна нулю  , тобто є зрівноваженою. Тут, наприклад, для системи двох сил:
, тобто є зрівноваженою. Тут, наприклад, для системи двох сил:  і
і 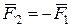 (рис. 5.22,а), буде:
(рис. 5.22,а), буде:  ;
;  (рис. 5.22,б); система сил
(рис. 5.22,б); система сил  .
.
 5.5.4. У загальному випадку, зведену в центрі О до головного вектора
5.5.4. У загальному випадку, зведену в центрі О до головного вектора  вихідну систему сил можна подальшими спрощеннями звести до однієї сили, рівнодійної
вихідну систему сил можна подальшими спрощеннями звести до однієї сили, рівнодійної  , яка прикладена, на відміну від п. 5.5.2 у новому центрі О 1 на відстані
, яка прикладена, на відміну від п. 5.5.2 у новому центрі О 1 на відстані  від точки О. Цей випадок повністю співпадає за доведенням з випадком приведення, який розглянуто стосовно довільної системи сил у просторі у п. 5.4.4.3 і на рис. 5.18. Наприклад, для зображеної на рис. 5.23,а системи трьох сил: (
від точки О. Цей випадок повністю співпадає за доведенням з випадком приведення, який розглянуто стосовно довільної системи сил у просторі у п. 5.4.4.3 і на рис. 5.18. Наприклад, для зображеної на рис. 5.23,а системи трьох сил: ( ) отримаємо у центрах приведення О, О 1:
) отримаємо у центрах приведення О, О 1:  (рис. 5.23,б);
(рис. 5.23,б);  ;
;  (рис. 5.23,в), система сил
(рис. 5.23,в), система сил  .
.




