Окремі випадки рівноваги системи сил
Рівновага довільної системи паралельних сил у просторі
У випадку, коли всі сили паралельні між собою (система паралельних сил), осі системи координат доцільно вибрати так, щоб одна з осей (наприклад вісь
Рис. 6.1
Тоді перші дві і остання умови (6.2) будуть виконуватись як тотожності, що дає наступні (три) умови рівноваги:
Отже, відповідно до (6.3), для рівноваги просторової системи паралельних сил необхідно і достатньо, щоб сума проекцій сил на вісь, паралельну силам, і суми моментів цих сил відносно двох інших координатних осей дорівнювали нулю. Умови рівноваги довільної плоскої системи сил Як відомо (п. 5.5), довільна система сил у площині в загальному випадку зводиться у центрі О до сили Для даної системи сил існують три окремі випадки рівноваги. Перша (основна) форма умов рівноваги. Припустимо, що площина дії системи сил
Рис. 6.2
Проекції сил системи, а також радіусів-векторів точок їх прикладання на вісь
Система (6.4) аналітичних (алгебраїчних) умов рівноваги твердого тіла формулюється таким чином: для рівноваги довільної системи сил у площині необхідно і достатньо, щоб суми проекцій усіх сил на кожну з координатних осей Ox i Oy і алгебраїчна сума їх моментів відносно осі Друга форма умов рівноваги. У даному випадку умови рівноваги формулюються так: для рівноваги довільної плоскої системи сил необхідно і достатньо, щоб алгебраїчні суми моментів сил відносно будь-яких двох точок у площині дії сил і сума проекцій цих сил на вісь, яка не перпендикулярна до прямої, що проходить через обрані точки, дорівнювали нулю. Для площини Е дії сил системи, точок В, С на ній і осі Ox (рис. 6.3) буде:
де
Рис. 6.3
Необхідність цих умов очевидна, бо якщо будь-яка з умов не буде виконуватися, то або в точці В головний вектор системи Достатність умов (6.5) доведемо наступним чином. Якщо виконуються тільки перші з двох умов (6.5), тобто Третя форма умов рівноваги. Ця форма умов рівноваги формулюється таким чином: для рівноваги довільної плоскої системи сил необхідно і достатньо, щоб алгебраїчні суми моментів усіх сил відносно будь-яких трьох точок, наприклад В,С,D, що не лежать на одній прямій, дорівнювали нулю (рис. 6.4):
де В,С,D - точки приведення системи сил.
Рис. 6.4
Необхідність цих умов, враховуючи (5.11), очевидна, бо при одночасному виконанні, наприклад двох перших умов, головний момент системи при Достатність умов (6.6) випливає з того, що при їх виконанні система сил не знаходилася б у рівновазі тільки у випадку, коли її відмінна від нуля рівнодійна
|

 ) була паралельна силам (рис. 6.1).
) була паралельна силам (рис. 6.1).
 ;
;  ;
;  . (6.3)
. (6.3)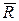 , яка дорівнює головному вектору
, яка дорівнює головному вектору  системи, і пари сил з моментом
системи, і пари сил з моментом  , який дорівнює головному моменту
, який дорівнює головному моменту  системи. При цьому головний вектор належить площині дії пари
системи. При цьому головний вектор належить площині дії пари  співпадає з координатною площиною
співпадає з координатною площиною  (рис. 6.2) системи координат
(рис. 6.2) системи координат  .
.
 ;
; 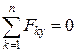 ;
; 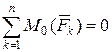 . (6.4)
. (6.4) ), дорівнювали нулю.
), дорівнювали нулю. ;
;  ;
;  , (6.5)
, (6.5) - проекція головного вектора системи сил у точці В на вісь Ох.
- проекція головного вектора системи сил у точці В на вісь Ох.
 0, або головний момент
0, або головний момент  0 (чи
0 (чи  ) і тоді рівноваги тіла не відбувається.
) і тоді рівноваги тіла не відбувається. і
і  , то така система сил може мати лише рівнодійну
, то така система сил може мати лише рівнодійну  (рис. 6.3), лінія дії якої проходить через точки В і С. Оскільки вісь Ox проходить під кутом
(рис. 6.3), лінія дії якої проходить через точки В і С. Оскільки вісь Ox проходить під кутом 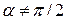 до відрізка ВС, то остання умова (6.5) може бути виконана тільки коли
до відрізка ВС, то остання умова (6.5) може бути виконана тільки коли  , тобто коли
, тобто коли  . Це призводить до одночасного виконання всіх умов (6.5), що забезпечують рівновагу тіла безумовно.
. Це призводить до одночасного виконання всіх умов (6.5), що забезпечують рівновагу тіла безумовно. , (6.6)
, (6.6)
 може дорівнювати нулю у третій точці D
може дорівнювати нулю у третій точці D  тільки коли головний вектор
тільки коли головний вектор  системи сил дорівнює нулю. Тому при одночасному виконанні умов (6.6) виконуються умови (6.1) рівноваги тіла і воно буде у рівновазі.
системи сил дорівнює нулю. Тому при одночасному виконанні умов (6.6) виконуються умови (6.1) рівноваги тіла і воно буде у рівновазі.


