Розглянемо тіло, яке, спираючись на шорстку поверхню, перебуває під дією рівнодійної зовнішніх активних сил  в стані рівноваги. У цьому випадку, враховуючи (7.2), буде виконуватись умова
в стані рівноваги. У цьому випадку, враховуючи (7.2), буде виконуватись умова
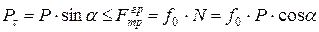
або  , (7.3)
, (7.3)
де  - дотична складова рівнодійної. У (7.3) враховано, що нормальна складова
- дотична складова рівнодійної. У (7.3) враховано, що нормальна складова  рівнодійної
рівнодійної 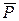 притискує тіло до поверхні і викликає відповідно реакцію
притискує тіло до поверхні і викликає відповідно реакцію  . При цьому граничну рівновагу тіла матимемо при
. При цьому граничну рівновагу тіла матимемо при  (випадок навантаження тіла зображено на рис. 7.3), тобто, враховуючи (7.3), коли
(випадок навантаження тіла зображено на рис. 7.3), тобто, враховуючи (7.3), коли  . Але якщо буде
. Але якщо буде  , то тіло почне рухатись. Виразимо далі умови рівноваги тіла через кут j 0 між реакцією
, то тіло почне рухатись. Виразимо далі умови рівноваги тіла через кут j 0 між реакцією 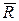 поверхні і її нормальною складовою
поверхні і її нормальною складовою  , який назвемо, при
, який назвемо, при  =
=  , кутом тертя j 0:
, кутом тертя j 0:

Рис. 7.3
 . (7.4)
. (7.4)
З (7.4), враховуючи властивості коефіцієнта тертя спокою, випливає незалежність кута тертя j0 від ваги тіла, тобто величини нормальної реакції  контактуючих тіл. Крім того з виразів (7.3) і (7.4) отримаємо, що тіло перебуває у стані рівноваги, коли для кутів між рівнодійною
контактуючих тіл. Крім того з виразів (7.3) і (7.4) отримаємо, що тіло перебуває у стані рівноваги, коли для кутів між рівнодійною 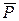 і нормаллю
і нормаллю  , а також реакцією
, а також реакцією 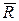 і тією ж нормаллю виконується нерівність
і тією ж нормаллю виконується нерівність
 , (7.5)
, (7.5)
а коли  (7.6)
(7.6)
тіло буде рухатись.
Тіло, спираючись на шорстку плоску поверхню, має можливість рухатись по ній під дією рівнодійної зовнішніх активних сил в будь-якому напрямку. Залежно від напрямків дії активних сил напрямок дотичної граничної реакції  буде змінюватись. При цьому вектор
буде змінюватись. При цьому вектор 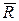 реакції поверхні, приймаючи його як рівнодійну, створить конічну поверхню, а його кінець при
реакції поверхні, приймаючи його як рівнодійну, створить конічну поверхню, а його кінець при  - підлогу прямого колового конуса. Прямий коловий конус, твірні якого з нормаллю до поверхні в даній точці складають кут тертя j0, називається конусом тертя (якщо коефіцієнт тертя
- підлогу прямого колового конуса. Прямий коловий конус, твірні якого з нормаллю до поверхні в даній точці складають кут тертя j0, називається конусом тертя (якщо коефіцієнт тертя  має у різних напрямках руху тіла різні значення, то конус тертя не буде прямим коловим).
має у різних напрямках руху тіла різні значення, то конус тертя не буде прямим коловим).
Незалежність нерівностей (7.5), (7.6) від параметрів рівнодійної 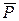 приводить до наступних умов спокою чи руху тіла стосовно конуса тертя. Якщо лінія дії рівнодійної активних сил проходить в середині конуса тертя або вздовж його твірної, то тіло перебуває в рівновазі (граничної рівноваги) при будь-яких величинах рівнодійної, а якщо лінія дії рівнодійної проходить поза конусом тертя, то тіло прийде до руху. Цю властивість використовують в техніці, наприклад, при визначенні геометричних характеристик кутів нахилу нарізки гвинтових з’єднань, що реалізують ефект самогальмування.
приводить до наступних умов спокою чи руху тіла стосовно конуса тертя. Якщо лінія дії рівнодійної активних сил проходить в середині конуса тертя або вздовж його твірної, то тіло перебуває в рівновазі (граничної рівноваги) при будь-яких величинах рівнодійної, а якщо лінія дії рівнодійної проходить поза конусом тертя, то тіло прийде до руху. Цю властивість використовують в техніці, наприклад, при визначенні геометричних характеристик кутів нахилу нарізки гвинтових з’єднань, що реалізують ефект самогальмування.

 в стані рівноваги. У цьому випадку, враховуючи (7.2), буде виконуватись умова
в стані рівноваги. У цьому випадку, враховуючи (7.2), буде виконуватись умова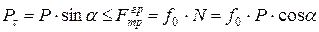
 , (7.3)
, (7.3) - дотична складова рівнодійної. У (7.3) враховано, що нормальна складова
- дотична складова рівнодійної. У (7.3) враховано, що нормальна складова  рівнодійної
рівнодійної 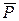 притискує тіло до поверхні і викликає відповідно реакцію
притискує тіло до поверхні і викликає відповідно реакцію  . При цьому граничну рівновагу тіла матимемо при
. При цьому граничну рівновагу тіла матимемо при  (випадок навантаження тіла зображено на рис. 7.3), тобто, враховуючи (7.3), коли
(випадок навантаження тіла зображено на рис. 7.3), тобто, враховуючи (7.3), коли  . Але якщо буде
. Але якщо буде  , то тіло почне рухатись. Виразимо далі умови рівноваги тіла через кут j 0 між реакцією
, то тіло почне рухатись. Виразимо далі умови рівноваги тіла через кут j 0 між реакцією 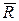 поверхні і її нормальною складовою
поверхні і її нормальною складовою  , який назвемо, при
, який назвемо, при  =
=  , кутом тертя j 0:
, кутом тертя j 0:
 . (7.4)
. (7.4) , (7.5)
, (7.5) (7.6)
(7.6) буде змінюватись. При цьому вектор
буде змінюватись. При цьому вектор  - підлогу прямого колового конуса. Прямий коловий конус, твірні якого з нормаллю до поверхні в даній точці складають кут тертя j0, називається конусом тертя (якщо коефіцієнт тертя
- підлогу прямого колового конуса. Прямий коловий конус, твірні якого з нормаллю до поверхні в даній точці складають кут тертя j0, називається конусом тертя (якщо коефіцієнт тертя  має у різних напрямках руху тіла різні значення, то конус тертя не буде прямим коловим).
має у різних напрямках руху тіла різні значення, то конус тертя не буде прямим коловим).


